Струјање подземних вода

Основна величина од које се полази у теорији струјања течности кроз порозно тло је потенцијал \(\phi\) дефинисан као

\[\phi = \frac{p}{\gamma} + h,\]

где је \(p\) притисак течности, \(\gamma\) специфична тежина, а \(h\) висина мерена у односу на изабрану референтну раван. Брзина течности \(\mathbf{q}\), позната и као Дарсијева брзина, представља запремину течности која прође у јединици времена кроз јединичну површину порозне средине. Она се може изразити помоћу потенцијала \(\phi\) релацијом која се зове Дарсијев закон:

\[\mathbf{q} = -\mathbf{K} \nabla \phi,\]

где је \(\mathbf{K}\) матрица пермеабилности која за ортотропни материјал има облик

\[\begin{split}\mathbf{K} = \begin{bmatrix} k_x & 0 & 0 \\ 0 & k_y & 0 \\ 0 & 0 & k_z \end{bmatrix},\end{split}\]

где су \(k_x\), \(k_y\) и \(k_z\) коефицијенти пермеабилности у одговарајућим правцима. Компонентни облик једначине је према томе:

\[\begin{split}q_x = -k_x \frac{\partial \phi}{\partial x}, \\ q_y = -k_y \frac{\partial \phi}{\partial y}, \\ q_z = -k_z \frac{\partial \phi}{\partial z}.\end{split}\]

Сада у систем уводимо једначину континуитета. У случају стационарног струјања нестишљивог флуида, каква је вода, једначина континуитета има облик

\[\nabla^T \mathbf{q} = 0,\]

или уз коришћење Дарсијевог закона

\[\frac{\partial}{\partial x}\left( k_x \frac{\partial \phi}{\partial x} \right) + \frac{\partial}{\partial y}\left( k_y \frac{\partial \phi}{\partial y} \right) + \frac{\partial}{\partial z}\left( k_z \frac{\partial \phi}{\partial z} \right) = 0\]

У случају када се промена коефицијената \(k_x, k_y, k_z\) са координатама може занемарити, што је најчешћи случај, једначина се своди на

\[k_x \frac{\partial^2\phi}{\partial x^2} + k_y \frac{\partial^2\phi}{\partial y^2} + k_z \frac{\partial^2\phi}{\partial z^2} = 0\]

Коначно, ако постоји извор и/или понор, за стационарне услове, хидродинамичка једначина има следећи облик:

(26)\[k_x \frac{\partial^2\phi}{\partial x^2} + k_y \frac{\partial^2\phi}{\partial y^2} + k_z \frac{\partial^2\phi}{\partial z^2} + \bar{Q}= 0\]

где је \(\bar{Q}\) запремински флукс (извор или понор, као количина течности по јединици запремине порозне средине у јединици времена). Гранични услови који се срећу у решавању проблема струјања кроз порозну средину описаног горњим једначинама приказани су на Сл. 25.

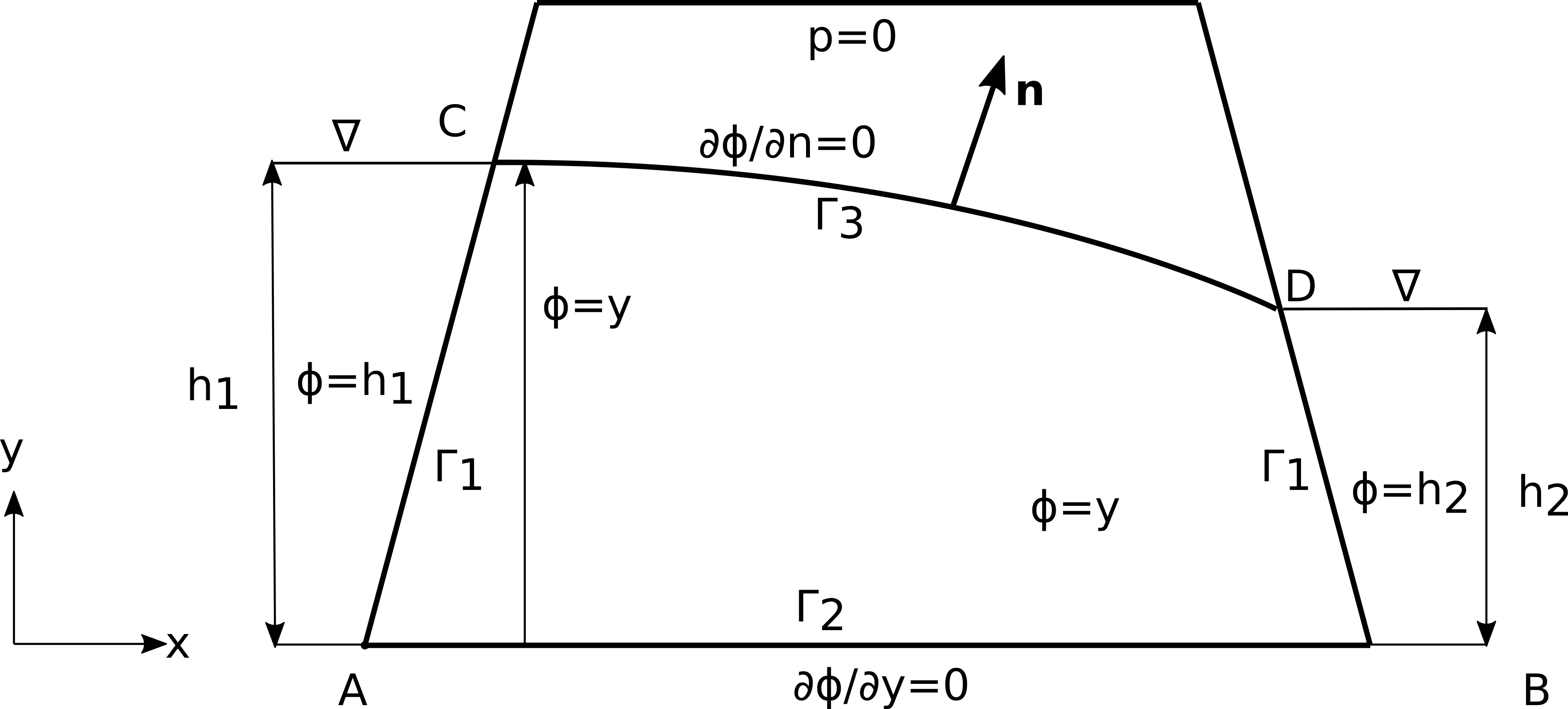
../_images/hidrologija-bc.png

Сл. 25 Различити гранични услови код проблема филтрације у две димензије.

Они могу бити:

  1. задати потенцијал
    \[\phi = \bar{\phi}, \qquad \mid \Gamma_1\]
  2. задати површински проток (флукс)
    \[q_n = \bar{q} \qquad \mid \Gamma_2\]

  3. слободна површина

    (27)\[p=0, \, \phi=y, \, \frac{\partial \phi}{\partial n}=0 \qquad \mid \Gamma_3\]

Приметимо да је на слободној површини \(\phi=y\). Пошто се облик слободне површине не зна, то је њено одређивање посебан задатак у овој области. И овај проблем ћемо покушати да покријемо методом НМПФЗ.

Стационарно струјање кроз порозну средину

Дводимензионално стационарно течење кроз порозни медијум је регулисано константном разликом потенцијала на две површине. Проток се јавља између два непропусна слоја у правоугаоној геометрији димензија 2m x 2m, као на Сл. 26.

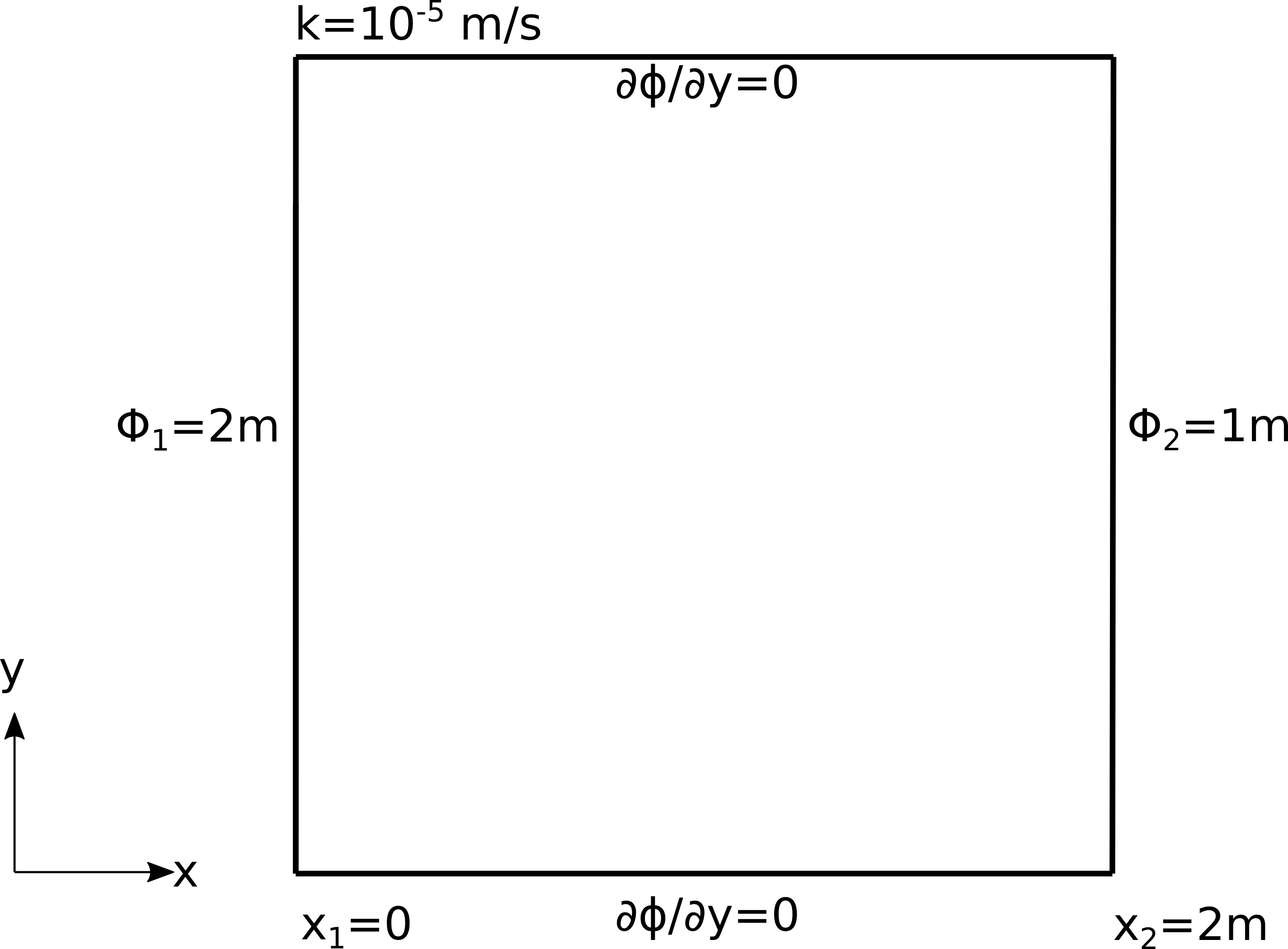
../_images/hidrologija-bc-bez-sp.png

Сл. 26 Поставка проблема стационарног струјања кроз порозну средину без слободне површине

Имплементација проблема је једноставна и њени најважнији делови се налазе на следећем листингу.

Листинг 6 Решење проблема струјања без слободне површине у 2Д коришћењем SCIANN библиотеке
 1# Osnovni grid
 2x_data, y_data = np.meshgrid(
 3    np.linspace(0, 2, 201),
 4    np.linspace(0, 2, 201)
 5)
 6
 7# Modeluje se phi(x,y)
 8x = sn.Variable('x')
 9y = sn.Variable('y')
10phi = sn.Functional('phi', [x,y], 4*[30], 'sigmoid')
11
12# %%
13k = 1.е-5
14TOL = 0.015
15
16# Osnovna jednacina
17fun1 = k * (diff(phi, x, order=2) + diff(phi, y, order=2))
18
19# Dirihleovi granicni uslovi
20C1 = (1-sign(x - (0+TOL))) * (phi-2)
21C2 = (1+sign(x - (2-TOL))) * (phi-1)
22
23# Njumanovi granicni uslovi
24N1 = (1-sign(y - (0+TOL))) * diff(phi,y)
25N2 = (1+sign(y - (2-TOL))) * diff(phi,y)
26
27# FZNN model
28m2 = sn.SciModel([x,y], [fun1, C1, C2, N1, N2],  optimizer='Adam')
29
30# Trening
31pinn_model = m2.train([x_data, y_data], 5*['zero'], learning_rate=0.001, batch_size=1024, epochs=100, stop_loss_value=1E-15)

Са свим овим поставкама смо се мање-више већ сретали, осим што до сада нисмо имали 2Д стационарни проблем. Постављамо равномерну мрежу колокационих тачака у димензијама домена (2m x 2m), затим дефинишем функционал \(\Phi(x,y)\) и диференцијалну једначину проблема. Приметимо да решење уопште не би требало да зависи од коефицијента \(k\). Следећи корак је поставка Дирихлеових граничних услова на левом (\(\Phi_1=2m\)) и на десном (\(\Phi_1=1m\)) крају домена, тј. на вертикалама \(x_1=0m\) и \(x=2m\), респективно:

C1 = (1-sign(x - (0+TOL))) * (phi-2)
C2 = (1+sign(x - (2-TOL))) * (phi-1)

Недостају само још Нојманови гранични услови који јамче да су доња (\(y=0\)) и горња (\(y=2m\)) површина непропусне, тј. да је извод потенцијала по \(y\) једнак нули:

N1 = (1-sign(y - (0+TOL))) * diff(phi,y)
N2 = (1+sign(y - (2-TOL))) * diff(phi,y)

Када се постави проблем, решење се назире већ за неколико десетина епоха тренирања. Аналитичко решење за потенцијал је, према Bear [Bea12]:

\[\phi = \Phi_1 - \frac{\Phi_1-\Phi_2}{L} (x-x_1)\]

где је \(L=x_2-x_1\). Дакле, поље потенцијала је константно у односу на \(Y\) осу, док је градијент потенцијала константан у правцу \(X\) осе.

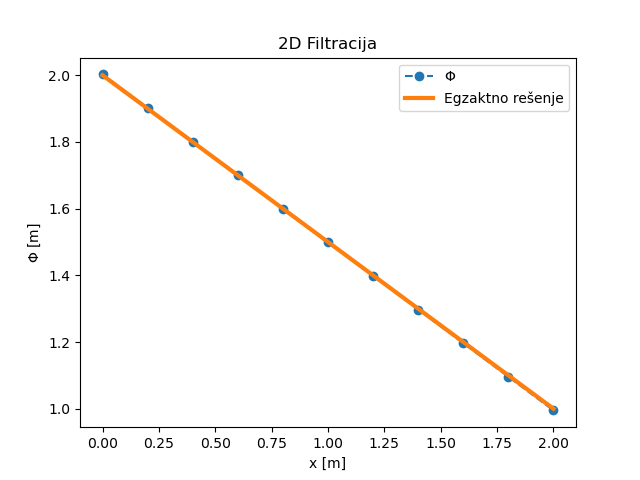
../_images/2d-filtracija-bez-sp1.png

Сл. 27 НМПФЗ решење потенцијала дуж \(X\) осе за 2Д случај струјања без слободне површине.

Поређење аналитичког и НМПФЗ решења је приказано на Сл. 27, а поље потенцијала је приказано на Сл. 28. Униформност потенцијалног поља у \(Y\) смеру, додатно потврђује тачност 2Д НМПФЗ решења за овај стационарни проблем.

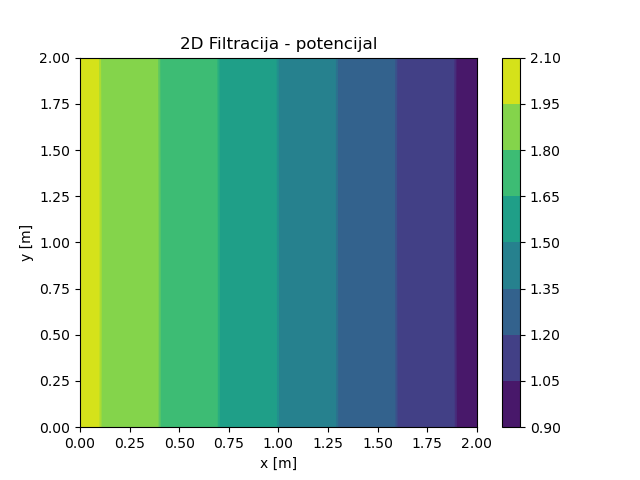
../_images/2d-filtracija-bez-sp2.png

Сл. 28 НМПФЗ решење поља потенцијала за 2Д случај струјања без слободне површине.

Стационарно струјање кроз порозну средину са слободном површином

Стационарно течење кроз порозни медијум, са слободном површином је регулисано константном разликом потенцијала на две супротне површине, као што је приказано на Сл. 29. Доња површина је непропусна. Геометријски и материјални подаци, као и гранични услови, такође су дати на Сл. 29.

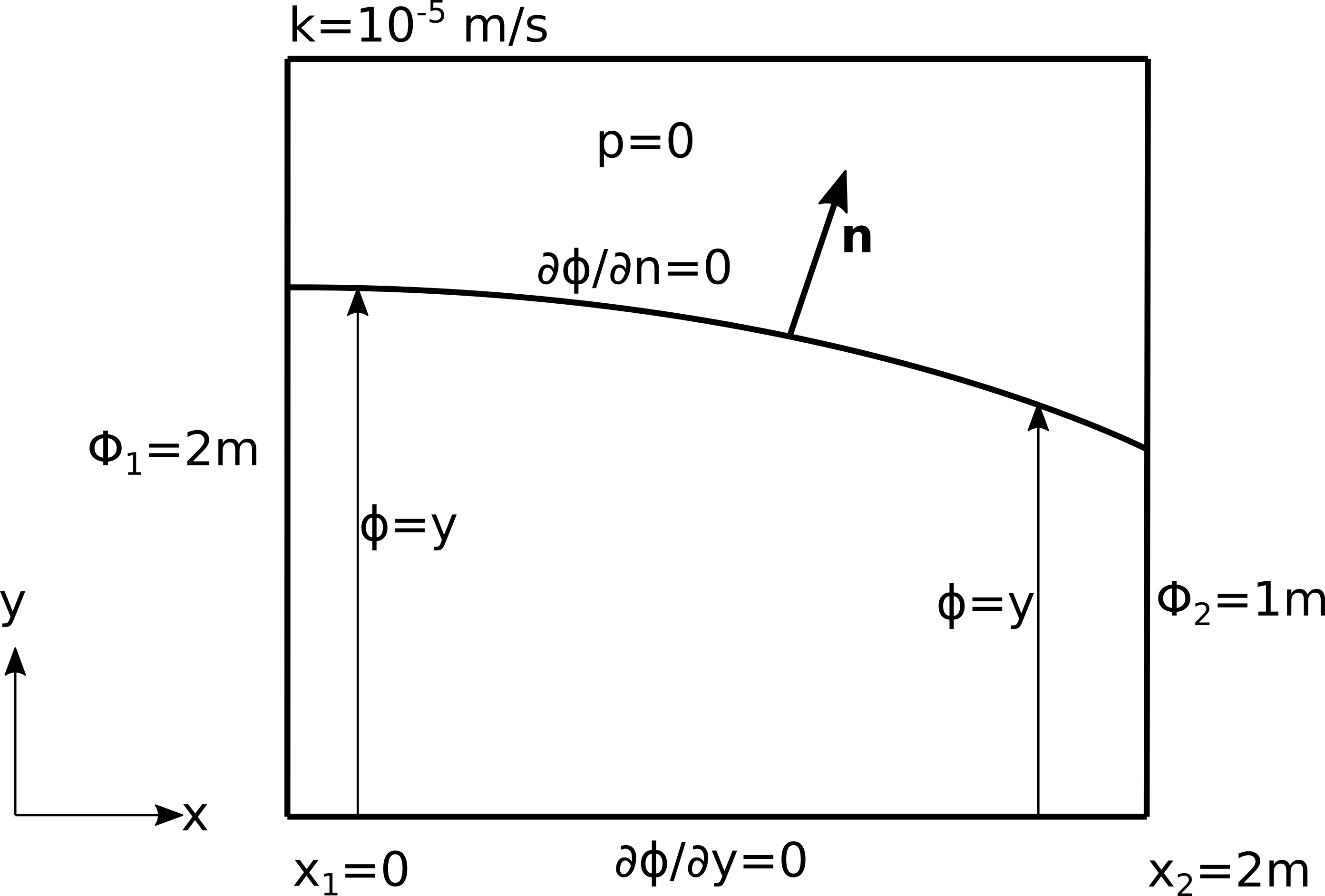
../_images/hidrologija-bc-sp.png

Сл. 29 Поставка проблема стационарног струјања кроз порозну средину са слободном површином

Вредности потенцијала у колокационим тачкама на површини \(x_1=0\) су \(\Phi_1=2m\) док су у тачкама на линији \(x_2=2m\) вредности \(\Phi_2=1m\). Доња површина је непропусна, па на њој задајемо да је градијент потенцијала нула. Дакле, и Дирихлеови и Нојманови гранични услови су идентични као и у претходном примеру који није укључивао постојање слободне површине. Међутим, њено постојање је физички нужно и дефинисано условима (27).

Како бисмо имплементирали овај гранични услов, морамо да израчунамо правац нормале:

k1 = diff(phi,x)
alpha = atan(k1)+np.pi/2
nx = cos(alpha)
ny = sin(alpha)

који ћемо добити тиме што додамо угао \(\frac{\pi}{2}\) правцу тангенте на phi, коју израчунавамо захваљујући тривијалној доступности првог извода у НМПФЗ методологији. Након тога лако израчунавамо компоненте нормале nx и ny. Гранични услов слободне површине постављамо на исти начин као и раније када смо користили библиотеку SCIANN, тако што се у виду конјункције наводи где услов важи и шта у том делу домена важи. Међутим, овог пута немамо строго дефинисане координате, јер положај слободне површине не знамо. Оно што знамо је да је на читавој слободној површини \(\phi=y\), па ово наводимо као област важења:

FS1 = (abs(y-phi)<0.009) * k * (diff(phi,x)*nx + diff(phi,y)*ny)

док услов непостојања протока кроз слободну површину \(\frac{\partial \phi}{\partial n} = \frac{\partial \phi}{\partial x} n_x + \frac{\partial \phi}{\partial y} n_y=0\) наводимо као главну компоненту.

Потребно је обезбедити и довољан број колокационих тачака да би се исправно испратио облик слободне површине. То ћемо обезбедити тако што у делу домена у коме очекујемо појаву слободне површине концентрацију колокационих тачака повећамо (у нашој имплементацији четири пута). Како је у питању чисто техничко решење, овде се тиме нећемо бавити, већ читаоца упућујемо на комплетан пример.

Аналитичко решење за потенцијал за овај једноставан проблем се по Bear [Bea12], може се написати у облику

\[\phi = \sqrt{\Phi_1^2 - 2B (x-x_1)},\]

где је

\[B = \frac{\Phi_1^2-\Phi_2^2}{2L}\]

и \(L=x_2-x_1\). Поређење НМПФЗ решења са аналитичким решењем може се видети на Сл. 30. Поље потенцијала је приказано на Сл. 31.

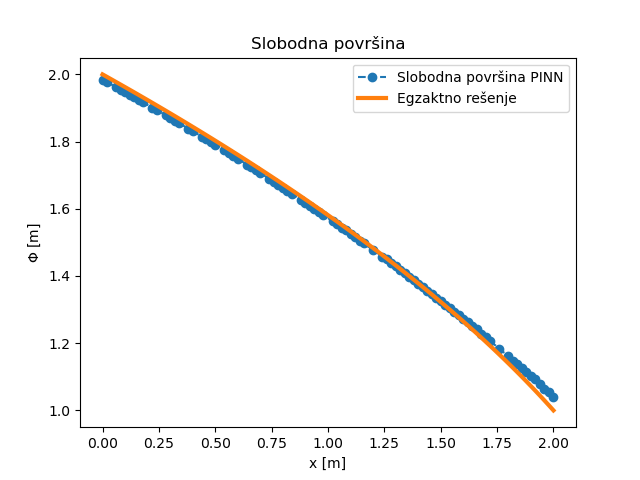
../_images/2d-filtracija-sp1.png

Сл. 30 НМПФЗ решење потенцијала дуж \(X\) осе за 2Д случај струјања са слободном површином.

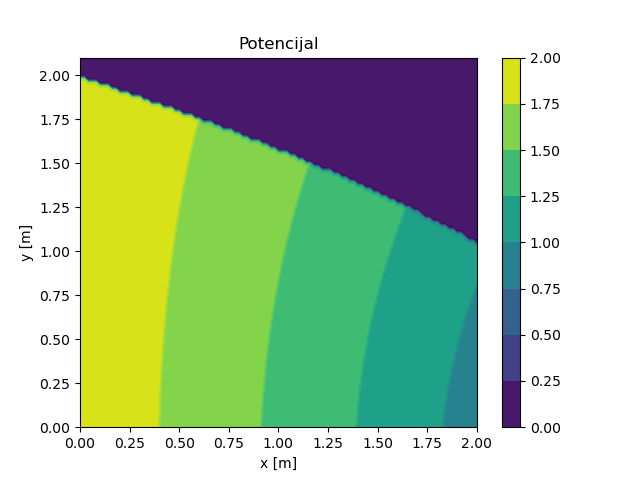
../_images/2d-filtracija-sp2.png

Сл. 31 НМПФЗ решење поља потенцијала за 2Д случај струјања са слободном површином.

Може се приметити релативно добро слагање НМПФЗ решења са аналитичким решењем, као и очигледна разлика распореда поља потенцијала у односу на случај без слободне површине приказан на Сл. 28. Ако пак упоредимо приступ решавању проблема слободне површине методом НМПФЗ са класичном методом коначних елемената код Kojić [Kojic98], можемо приметити да је НМПФЗ приступ једноставнији. Разлог томе је што се код НМПФЗ не захтева никакав посебан нумерички третман и употреба нумеричких претпоставки, већ се физика проблема директним путем преводи у НМПФЗ гранични услов.