ГРАФ
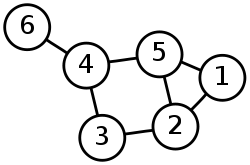
У рачунарству, граф је врста структуре података, тачније апстрактан тип података, који се састоји од скупа чворова и скупа грана, које представљају односе (везе) између чворова. Граф као структура података директно потиче од математичког концепта графа.
Граф G се дефинише на следећи начин: G=(V,E), где је V коначан, непразан скуп чворова, а E је скуп грана (веза између чворова). Када гране графа немају одређен смер, тада граф називамо неусмереним, а у супротном је граф усмерен. У пракси, за сваки чвор и грану везујемо неке податке са којима желимо да манипулишемо.
Избори репрезентације
Графови се у рачунарству представљају на разне начине. Најчешћи су листа повезаности и матрица повезаности. Листа повезаности је имплементирана тако што представља сваки чвор као структуру података која садржи листу свих суседних чворова. Матрица повезаности је матрица, чије врсте и колоне представљају почетне и крајње чворове, а дати члан матрице представља индикацију да ли између одговарајућа два чвора постоји грана (рецимо 0 ако не постоји, а 1 ако постоји). Листе повезаности се чешће користе код ретких графова, а у супротном су матрице повезаности добар избор. Такође, за врло велике графове који имају неку правилност што се тиче положаја грана, могући избор представљања је симболички граф. Ређе се за представљање графа користи матрица инциденције. Врсте ове матрице представљају чворове, а колоне представљају гране. У свакој колони стоје јединице на местима која одговарају чворовима које спаја одговарајућа грана (а на осталим местима су нуле).
Поређење са другим структурама података
Графовске структуре података су не-хијерархијске, и стога су погодне за податке где су појединачни елементи повезани на комплексне начине. На пример, симулација рачунарске мреже се може спровести помоћу графа.
Хијерархијски скупови података се могу представити бинарним или небинарним стаблом. Стабла се такође могу посматрати и као графови.
Операције
Графовски алгоритми су од великог значаја у рачунарству. Типичне операције повезане са графовима су налажење пута између два чвора, за шта се на пример користе претрага графа у дубину и претрага графа у ширину, и налажење најкраћег пута од једног до другог чвора, за шта се може користити Дијкстра алгоритам1)
Теорија графова
Теорија графова је област математике, веома заступљена и у информатици, чија је област истраживање особина графова. Неформално говорећи, графови су састављени од тачака, односно чворова (врхова), и линија међу њима, односно грана.
Веома је честа употреба графова за опис модела или структура података. Структура једне веб презентације се може представити сликовито употребом графа. Чворови тог графа су поједине странице а гране графа су везе којима се може са једне странице прелазити на другу.
Проучавање алгоритама који решавају проблеме употребом графова представља веома значајан део информатичке науке. Мреже имају много примена у проучавању практичних аспеката теорије графова и то се зове анализа мрежа. Анализа мрежа је посебно значајна за проблеме моделирања и анализирање мрежног саобраћаја, рецимо Интернета.
1 function Dijkstra(G, w, s) 2 for each vertex v in V[G] // Иницијализација 3 d[v] := infinity 4 previous[v] := undefined 5 d[s] := 0 6 S := empty set 7 Q := V[G] 8 while Q is not an empty set // Дајкстрин алгоритам 9 u := Extract_Min(Q) 10 S := S union {u} 11 for each edge (u,v) outgoing from u 12 if d[u] + w(u,v) < d[v] // Ослобађање ивице (u,v) 13 d[v] := d[u] + w(u,v) 14 Q := Q union {v} 15 previous[v] := u