Strujanje podzemnih voda

Osnovna veličina od koje se polazi u teoriji strujanja tečnosti kroz porozno tlo je potencijal \(\phi\) definisan kao

\[\phi = \frac{p}{\gamma} + h,\]

gde je \(p\) pritisak tečnosti, \(\gamma\) specifična težina, a \(h\) visina merena u odnosu na izabranu referentnu ravan. Brzina tečnosti \(\mathbf{q}\), poznata i kao Darsijeva brzina, predstavlja zapreminu tečnosti koja prođe u jedinici vremena kroz jediničnu površinu porozne sredine. Ona se može izraziti pomoću potencijala \(\phi\) relacijom koja se zove Darsijev zakon:

\[\mathbf{q} = -\mathbf{K} \nabla \phi,\]

gde je \(\mathbf{K}\) matrica permeabilnosti koja za ortotropni materijal ima oblik

\[\begin{split}\mathbf{K} = \begin{bmatrix} k_x & 0 & 0 \\ 0 & k_y & 0 \\ 0 & 0 & k_z \end{bmatrix},\end{split}\]

gde su \(k_x\), \(k_y\) i \(k_z\) koeficijenti permeabilnosti u odgovarajućim pravcima. Komponentni oblik jednačine je prema tome:

\[\begin{split}q_x = -k_x \frac{\partial \phi}{\partial x}, \\ q_y = -k_y \frac{\partial \phi}{\partial y}, \\ q_z = -k_z \frac{\partial \phi}{\partial z}.\end{split}\]

Sada u sistem uvodimo jednačinu kontinuiteta. U slučaju stacionarnog strujanja nestišljivog fluida, kakva je voda, jednačina kontinuiteta ima oblik

\[\nabla^T \mathbf{q} = 0,\]

ili uz korišćenje Darsijevog zakona

\[\frac{\partial}{\partial x}\left( k_x \frac{\partial \phi}{\partial x} \right) + \frac{\partial}{\partial y}\left( k_y \frac{\partial \phi}{\partial y} \right) + \frac{\partial}{\partial z}\left( k_z \frac{\partial \phi}{\partial z} \right) = 0\]

U slučaju kada se promena koeficijenata \(k_x, k_y, k_z\) sa koordinatama može zanemariti, što je najčešći slučaj, jednačina se svodi na

\[k_x \frac{\partial^2\phi}{\partial x^2} + k_y \frac{\partial^2\phi}{\partial y^2} + k_z \frac{\partial^2\phi}{\partial z^2} = 0\]

Konačno, ako postoji izvor i/ili ponor, za stacionarne uslove, hidrodinamička jednačina ima sledeći oblik:

(26)\[k_x \frac{\partial^2\phi}{\partial x^2} + k_y \frac{\partial^2\phi}{\partial y^2} + k_z \frac{\partial^2\phi}{\partial z^2} + \bar{Q}= 0\]

gde je \(\bar{Q}\) zapreminski fluks (izvor ili ponor, kao količina tečnosti po jedinici zapremine porozne sredine u jedinici vremena). Granični uslovi koji se sreću u rešavanju problema strujanja kroz poroznu sredinu opisanog gornjim jednačinama prikazani su na Sl. 25.

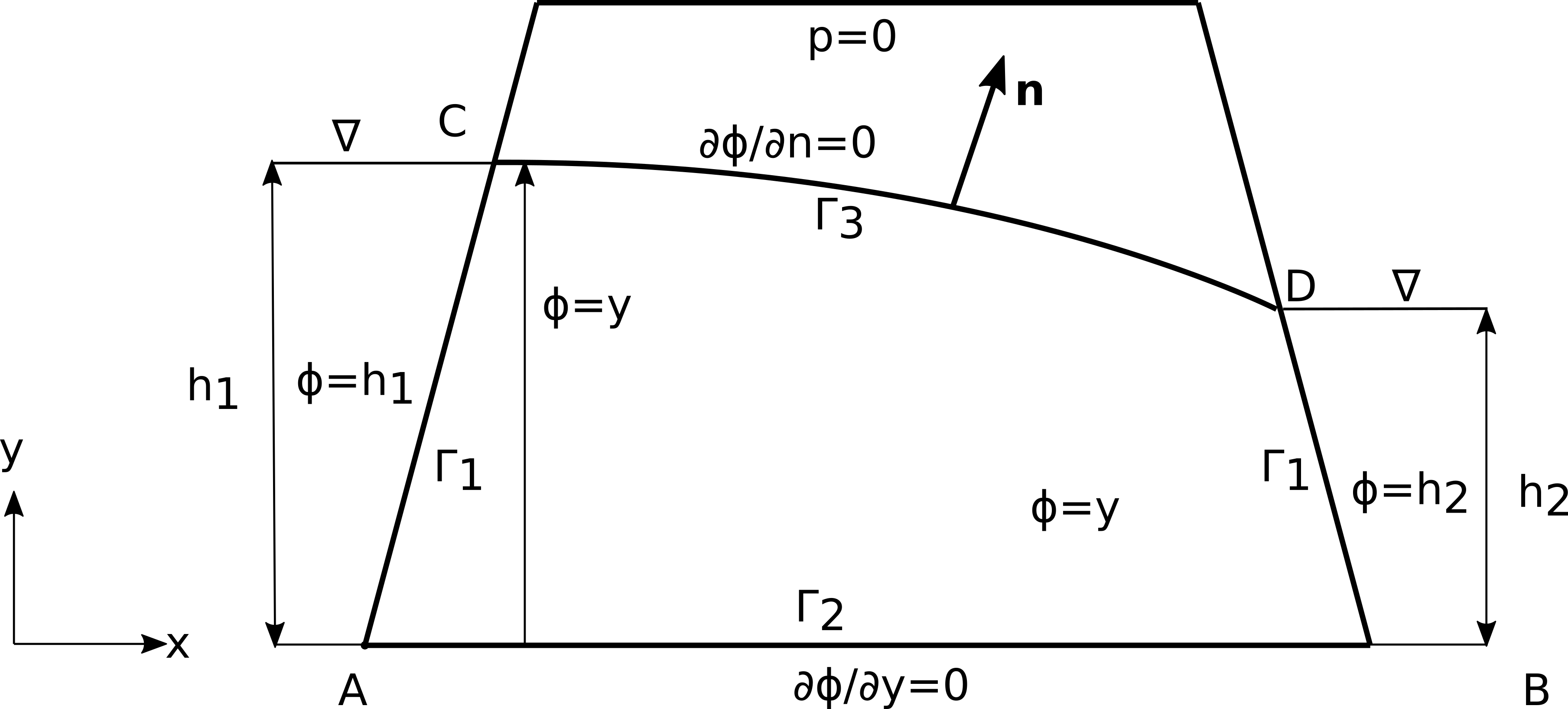
Sl. 25 Različiti granični uslovi kod problema filtracije u dve dimenzije.

Oni mogu biti:

1. zadati potencijal

   \[\phi = \bar{\phi}, \qquad \mid \Gamma_1\]

2. zadati površinski protok (fluks)

   \[q_n = \bar{q} \qquad \mid \Gamma_2\]

3. slobodna površina

   (27)\[p=0, \, \phi=y, \, \frac{\partial \phi}{\partial n}=0 \qquad \mid \Gamma_3\]

Primetimo da je na slobodnoj površini \(\phi=y\). Pošto se oblik slobodne površine ne zna, to je njeno određivanje poseban zadatak u ovoj oblasti. I ovaj problem ćemo pokušati da pokrijemo metodom NMPFZ.

Stacionarno strujanje kroz poroznu sredinu

Dvodimenzionalno stacionarno tečenje kroz porozni medijum je regulisano konstantnom razlikom potencijala na dve površine. Protok se javlja između dva nepropusna sloja u pravougaonoj geometriji dimenzija 2m x 2m, kao na Sl. 26.

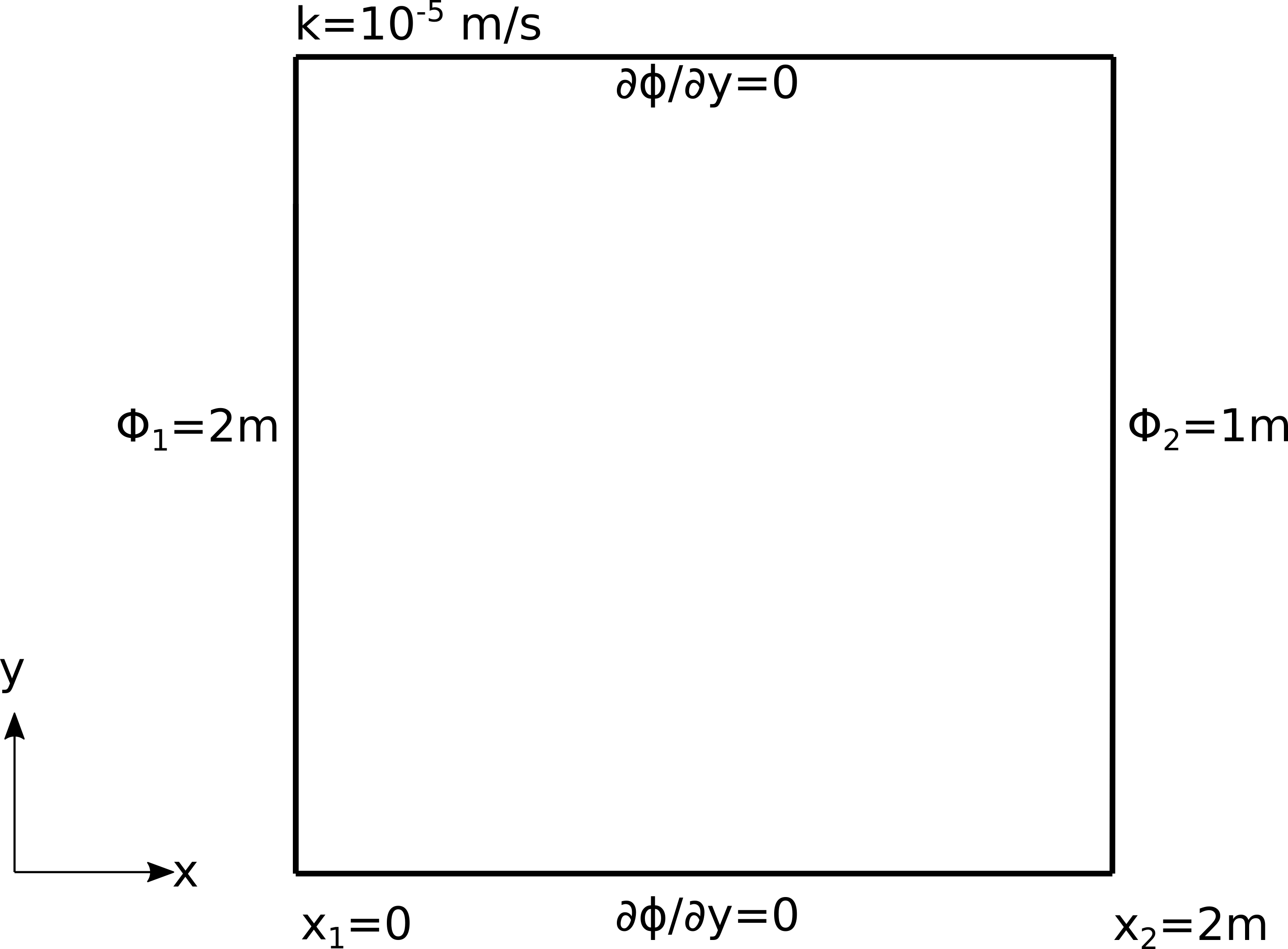
Sl. 26 Postavka problema stacionarnog strujanja kroz poroznu sredinu bez slobodne površine

Implementacija problema je jednostavna i njeni najvažniji delovi se nalaze na sledećem listingu.

Listing 6 Rešenje problema strujanja bez slobodne površine u 2D korišćenjem SCIANN biblioteke

# Osnovni grid
x_data, y_data = np.meshgrid(
    np.linspace(0, 2, 201),
    np.linspace(0, 2, 201)
)

# Modeluje se phi(x,y)
x = sn.Variable('x')
y = sn.Variable('y')
phi = sn.Functional('phi', [x,y], 4*[30], 'sigmoid')

# %%
k = 1.e-5
TOL = 0.015

# Osnovna jednacina
fun1 = k * (diff(phi, x, order=2) + diff(phi, y, order=2))

# Dirihleovi granicni uslovi
C1 = (1-sign(x - (0+TOL))) * (phi-2)
C2 = (1+sign(x - (2-TOL))) * (phi-1)

# Njumanovi granicni uslovi
N1 = (1-sign(y - (0+TOL))) * diff(phi,y)
N2 = (1+sign(y - (2-TOL))) * diff(phi,y)

# FZNN model
m2 = sn.SciModel([x,y], [fun1, C1, C2, N1, N2],  optimizer='Adam')

# Trening
pinn_model = m2.train([x_data, y_data], 5*['zero'], learning_rate=0.001, batch_size=1024, epochs=100, stop_loss_value=1E-15)

Sa svim ovim postavkama smo se manje-više već sretali, osim što do sada nismo imali 2D stacionarni problem. Postavljamo ravnomernu mrežu kolokacionih tačaka u dimenzijama domena (2m x 2m), zatim definišem funkcional \(\Phi(x,y)\) i diferencijalnu jednačinu problema. Primetimo da rešenje uopšte ne bi trebalo da zavisi od koeficijenta \(k\). Sledeći korak je postavka Dirihleovih graničnih uslova na levom (\(\Phi_1=2m\)) i na desnom (\(\Phi_1=1m\)) kraju domena, tj. na vertikalama \(x_1=0m\) i \(x=2m\), respektivno:

C1 = (1-sign(x - (0+TOL))) * (phi-2)
C2 = (1+sign(x - (2-TOL))) * (phi-1)

Nedostaju samo još Nojmanovi granični uslovi koji jamče da su donja (\(y=0\)) i gornja (\(y=2m\)) površina nepropusne, tj. da je izvod potencijala po \(y\) jednak nuli:

N1 = (1-sign(y - (0+TOL))) * diff(phi,y)
N2 = (1+sign(y - (2-TOL))) * diff(phi,y)

Kada se postavi problem, rešenje se nazire već za nekoliko desetina epoha treniranja. Analitičko rešenje za potencijal je, prema Bear [Bea12]:

\[\phi = \Phi_1 - \frac{\Phi_1-\Phi_2}{L} (x-x_1)\]

gde je \(L=x_2-x_1\). Dakle, polje potencijala je konstantno u odnosu na \(Y\) osu, dok je gradijent potencijala konstantan u pravcu \(X\) ose.

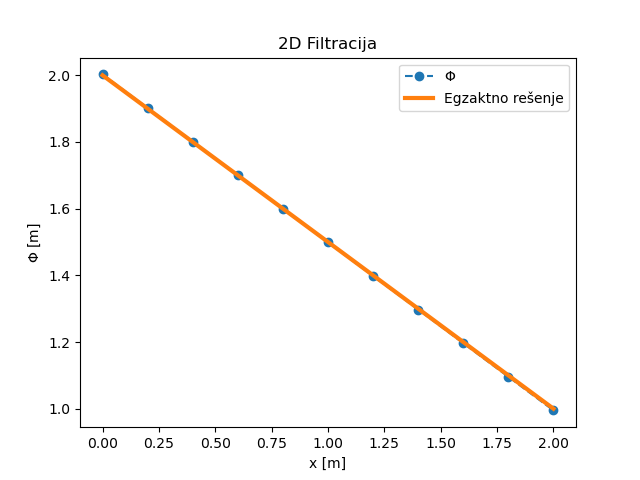
Sl. 27 NMPFZ rešenje potencijala duž \(X\) ose za 2D slučaj strujanja bez slobodne površine.

Poređenje analitičkog i NMPFZ rešenja je prikazano na Sl. 27, a polje potencijala je prikazano na Sl. 28. Uniformnost potencijalnog polja u \(Y\) smeru, dodatno potvrđuje tačnost 2D NMPFZ rešenja za ovaj stacionarni problem.

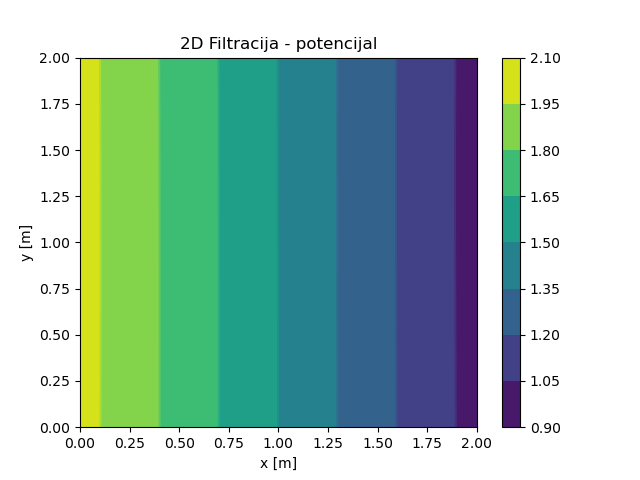
Sl. 28 NMPFZ rešenje polja potencijala za 2D slučaj strujanja bez slobodne površine.

Stacionarno strujanje kroz poroznu sredinu sa slobodnom površinom

Stacionarno tečenje kroz porozni medijum, sa slobodnom površinom je regulisano konstantnom razlikom potencijala na dve suprotne površine, kao što je prikazano na Sl. 29. Donja površina je nepropusna. Geometrijski i materijalni podaci, kao i granični uslovi, takođe su dati na Sl. 29.

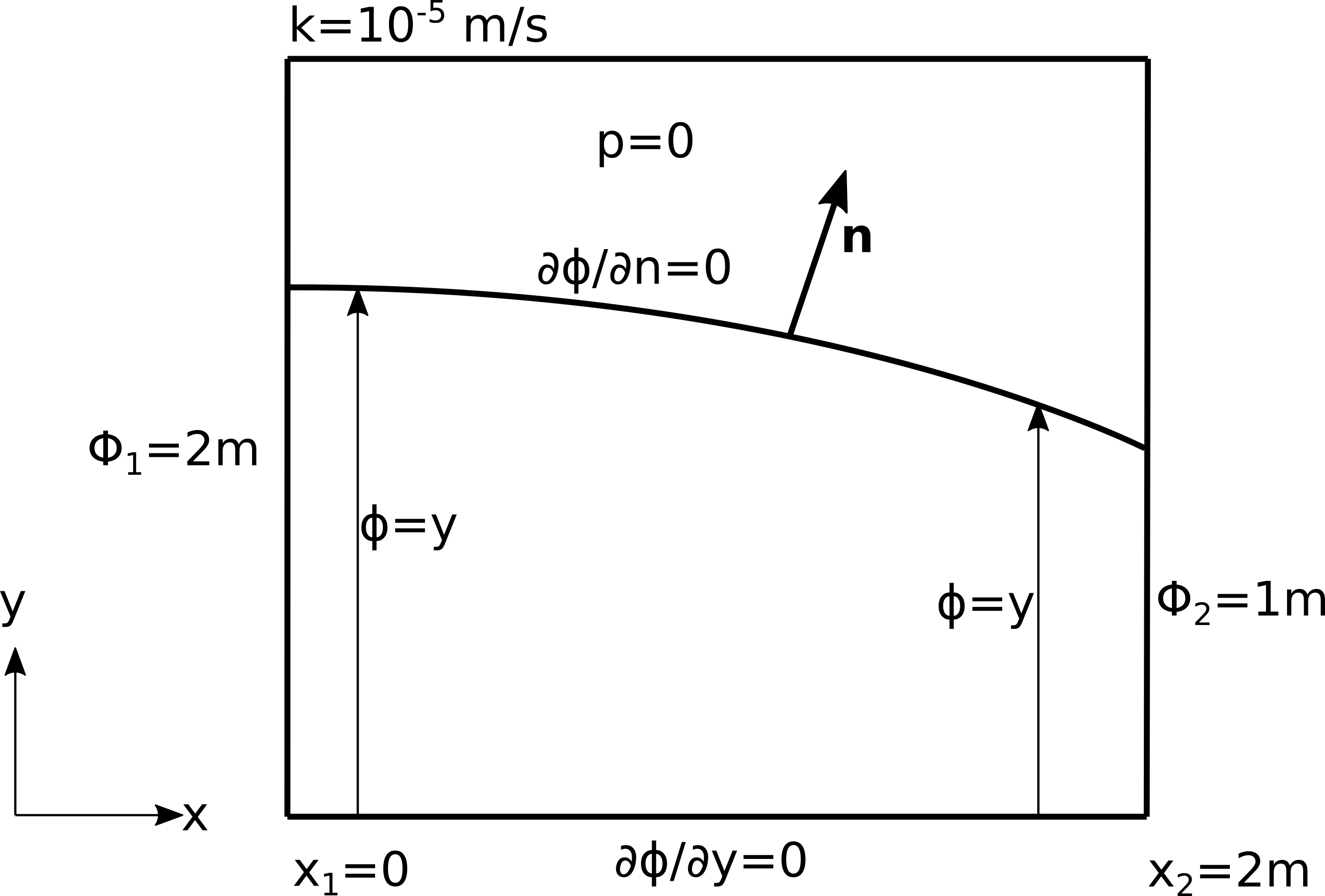
Sl. 29 Postavka problema stacionarnog strujanja kroz poroznu sredinu sa slobodnom površinom

Vrednosti potencijala u kolokacionim tačkama na površini \(x_1=0\) su \(\Phi_1=2m\) dok su u tačkama na liniji \(x_2=2m\) vrednosti \(\Phi_2=1m\). Donja površina je nepropusna, pa na njoj zadajemo da je gradijent potencijala nula. Dakle, i Dirihleovi i Nojmanovi granični uslovi su identični kao i u prethodnom primeru koji nije uključivao postojanje slobodne površine. Međutim, njeno postojanje je fizički nužno i definisano uslovima (27).

Kako bismo implementirali ovaj granični uslov, moramo da izračunamo pravac normale:

k1 = diff(phi,x)
alpha = atan(k1)+np.pi/2
nx = cos(alpha)
ny = sin(alpha)

koji ćemo dobiti time što dodamo ugao \(\frac{\pi}{2}\) pravcu tangente na phi, koju izračunavamo zahvaljujući trivijalnoj dostupnosti prvog izvoda u NMPFZ metodologiji. Nakon toga lako izračunavamo komponente normale nx i ny. Granični uslov slobodne površine postavljamo na isti način kao i ranije kada smo koristili biblioteku SCIANN, tako što se u vidu konjunkcije navodi gde uslov važi i šta u tom delu domena važi. Međutim, ovog puta nemamo strogo definisane koordinate, jer položaj slobodne površine ne znamo. Ono što znamo je da je na čitavoj slobodnoj površini \(\phi=y\), pa ovo navodimo kao oblast važenja:

FS1 = (abs(y-phi)<0.009) * k * (diff(phi,x)*nx + diff(phi,y)*ny)

dok uslov nepostojanja protoka kroz slobodnu površinu \(\frac{\partial \phi}{\partial n} = \frac{\partial \phi}{\partial x} n_x + \frac{\partial \phi}{\partial y} n_y=0\) navodimo kao glavnu komponentu.

Potrebno je obezbediti i dovoljan broj kolokacionih tačaka da bi se ispravno ispratio oblik slobodne površine. To ćemo obezbediti tako što u delu domena u kome očekujemo pojavu slobodne površine koncentraciju kolokacionih tačaka povećamo (u našoj implementaciji četiri puta). Kako je u pitanju čisto tehničko rešenje, ovde se time nećemo baviti, već čitaoca upućujemo na kompletan primer.

Analitičko rešenje za potencijal za ovaj jednostavan problem se po Bear [Bea12], može se napisati u obliku

\[\phi = \sqrt{\Phi_1^2 - 2B (x-x_1)},\]

gde je

\[B = \frac{\Phi_1^2-\Phi_2^2}{2L}\]

i \(L=x_2-x_1\). Poređenje NMPFZ rešenja sa analitičkim rešenjem može se videti na Sl. 30. Polje potencijala je prikazano na Sl. 31.

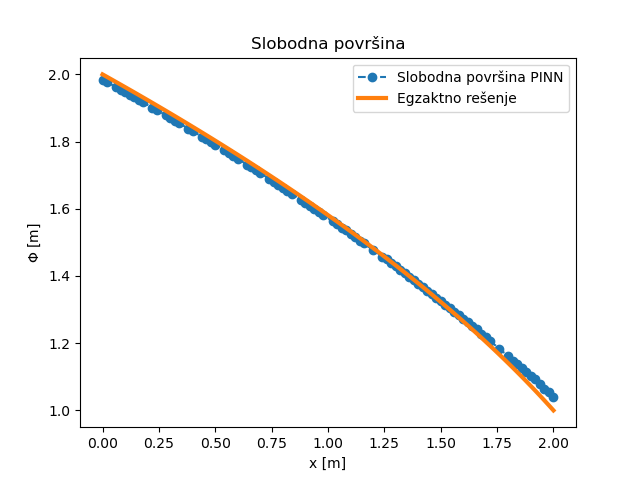
Sl. 30 NMPFZ rešenje potencijala duž \(X\) ose za 2D slučaj strujanja sa slobodnom površinom.

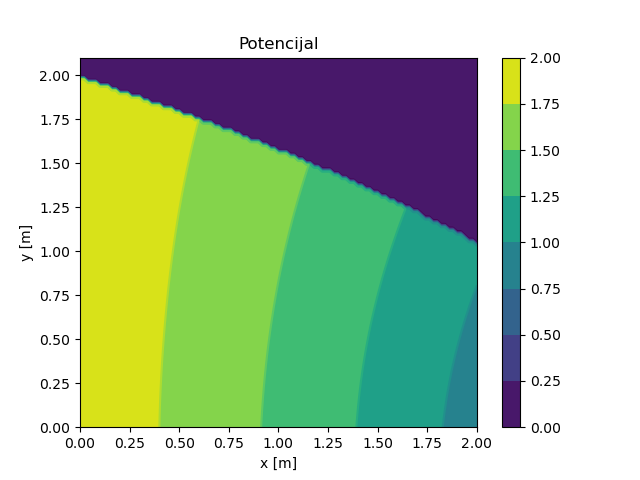
Sl. 31 NMPFZ rešenje polja potencijala za 2D slučaj strujanja sa slobodnom površinom.

Može se primetiti relativno dobro slaganje NMPFZ rešenja sa analitičkim rešenjem, kao i očigledna razlika rasporeda polja potencijala u odnosu na slučaj bez slobodne površine prikazan na Sl. 28. Ako pak uporedimo pristup rešavanju problema slobodne površine metodom NMPFZ sa klasičnom metodom konačnih elemenata kod Kojić [Kojic98], možemo primetiti da je NMPFZ pristup jednostavniji. Razlog tome je što se kod NMPFZ ne zahteva nikakav poseban numerički tretman i upotreba numeričkih pretpostavki, već se fizika problema direktnim putem prevodi u NMPFZ granični uslov.