Propagacija talasa u otvorenom kanalu

Upravljanje vodnim resursima zahteva alate za dugoročno i kratkoročno predviđanje različitih hidroloških fenomena. Predviđanje je značajno u oblastima upravljanja rizikom od poplava, upravljanja hidro-elektranama, unutrašnje plovidbe, vodosnabdevanja, itd. Brojni zadaci u vezi sa predviđanjem hidroloških podataka uspešno su obrađeni korišćenjem pristupa predviđanja zasnovanog na klasičnom numeričkom modelovanju. Iako ovaj pristup daje zadovoljavajuće rezultate, još uvek ima mnogo problema koje treba rešiti. U mnogim slučajevima, vreme izračunavanja je parametar koji može ograničiti primenu fizički zasnovanih hidroloških i hidrauličkih modela u realnoj primeni. Pored toga, fizički zasnovani modeli su nedovoljno fleksibilni u slučajevima inverznih problema, identifikacije parametara, asimilacije merenih podataka itd.

Modeli predviđanja zasnovani na neuronskim mrežama primenjeni su u modelovanju padavina i oticaja Chadalawada et al. [CHB20], sistemima ranog upozorenja na poplave Duncan et al. [DCK+13], kao i modelovanju urbanih vodovodnih mreža Garzón et al. [GarzonKLT22]. Ovi pristupi zahtevaju veliku količinu podataka za obuku, što može stvoriti probleme ukoliko nema dovoljno podataka. Pored toga, može se primetiti da ova vrsta modela nije u stanju da isporuči dobre rezultate kada ulazni podaci izlaze izvan opsega podataka koji se koriste za obuku. U ovim slučajevima, modeli zasnovani na neuronskim mrežama mogu proizvesti fizički nemoguće rezultate. U poslednjih nekoliko godina, ubrzano se uvodi NMPFZ pristup i u ovoj oblasti. U narednom primeru ćemo sagledati potencijal upotrebe NMPFZ u jednodimenzionom problemu propagacije poplavnog talasa u otvorenim kanalima spajanjem fizičkog zakona sa početnim i graničnim uslovima opisanim kinematičkom jednačinom propagacije talasa.

Usmeravanje poplava - fizički zakoni

Prostiranje poplavnog talasa u otvorenim kanalima je opisano pomoću dve jednačine, i to jednačinom kontinuiteta (28) i zakonom održanja količine kretanja (29). Ova jednačina sadrži uticaje trenja, gravitacije, sile pritiska, kao i lokalnog i konvektivnog ubrzanja. U ovom primeru, prostiranje talasa u pravougaonom kanalu je predstavljeno kinematičkim talasom koji pojednostavljuje dinamičku jednačinu, uzimajući samo uticaj trenja i gravitacije:

(28)\[\frac{\partial h(x,t)}{\partial t} + c \frac{\partial h(x,t)}{\partial x} = 0\]

(29)\[Q(x,t) = \frac{1}{n} \cdot B \cdot h(x,t)^\frac{5}{3} \cdot \sqrt{I_d},\]

gde \(h \, [m]\) predstavlja dubinu vode, \(t \, [s]\) je vreme, \(x \, [m]\) prostornu koordinatu, \(c \, [m/s]\) brzinu propagacije poremećaja, \(Q [m^3/s]\) protok, \(n [m^{-\frac{1}{3}}s]\) reprezentuje Maningovu hrapavost, \(B \, [m]\) širinu poprečnog preseka i \(I_d\) nagib po uzdužnoj osi.

Cilj modelovanja prostiranja talasa je procena promene dubine vode duž kanala \(h(x,t)\) koja je izazvana poplavnim talasom predstavljenim hidrogramom toka \(Q_{in}(t) = Q(0,t)\) na uzvodnom kraju kanala.

Konstrukcija funkcije gubitka

Ako se osvrnemo na opšti izraz za funkciju gubitka (2), vidimo tri komponente, i to gubitak koji potiče od rezidualne mreže, gubitak koji potiče od početnih uslova i gubitak koji potiče od graničnih uslova. Krenimo redom. Komponenta funkcije gubitka koja potiče od diferencijalne jednačine (28) definisana je desnom stranom iste jednačine. Komponenta početnih uslova se definiše kao:

\[h(x,t=0) = h_0\]

Pored toga, potreban nam je i granični uslov koji definiše vrednost visine talasa na početku modelovanog domena, tj. na \(x=0\) odakle talas dolazi. Taj granični uslov izvodimo iz dinamičke jednačine (29):

\[h(0,t) = \left( \frac{Q_{in}(t) \cdot n}{B \cdot \sqrt{I_d}} \right)^\frac{3}{5}.\]

Ukoliko kao meru greške usvojimo srednju kvadratnu grešku (Mean Squared Error - MSE), kompozitna funkcija gubitka izgledaće ovako:

\[MSE = MSE_r + MSE_0 + MSE_b,\]

gde su:

\[\begin{split}MSE_r = \frac{1}{N_{x_f,t_f}} \sum \left| r(x_f, t_f) \right|^2, \\ MSE_0 = \frac{1}{N_{x_0,t_0}} \sum \left| \tilde{h}(x_0,0)-h(x_0,0) \right|^2, \\ MSE_b = \frac{1}{N_{x_b,t_b}} \sum \left| \tilde{h}(0,t_b)-h(0,t_b) \right|^2.\end{split}\]

Ovde su \(N_{x_f,t_f}\), \(N_{x_0,t_0}\) i \(N_{x_b,t_b}\) ukupni brojevi kolokacionih tačaka u unutrašnjosti modelovanog domena, za početne i za granične uslove, respektivno.

Test primer i implementacija

Primer na kome ćemo testirati valjanost našeg NMPFZ pristupa za modelovanje širenja poplavnog talasa je propagacija talasa duž kanala dugog 1600 metara, oblika prizme i pravougaonog poprečnog preseka širokog 15 metara, kao na Sl. 32.

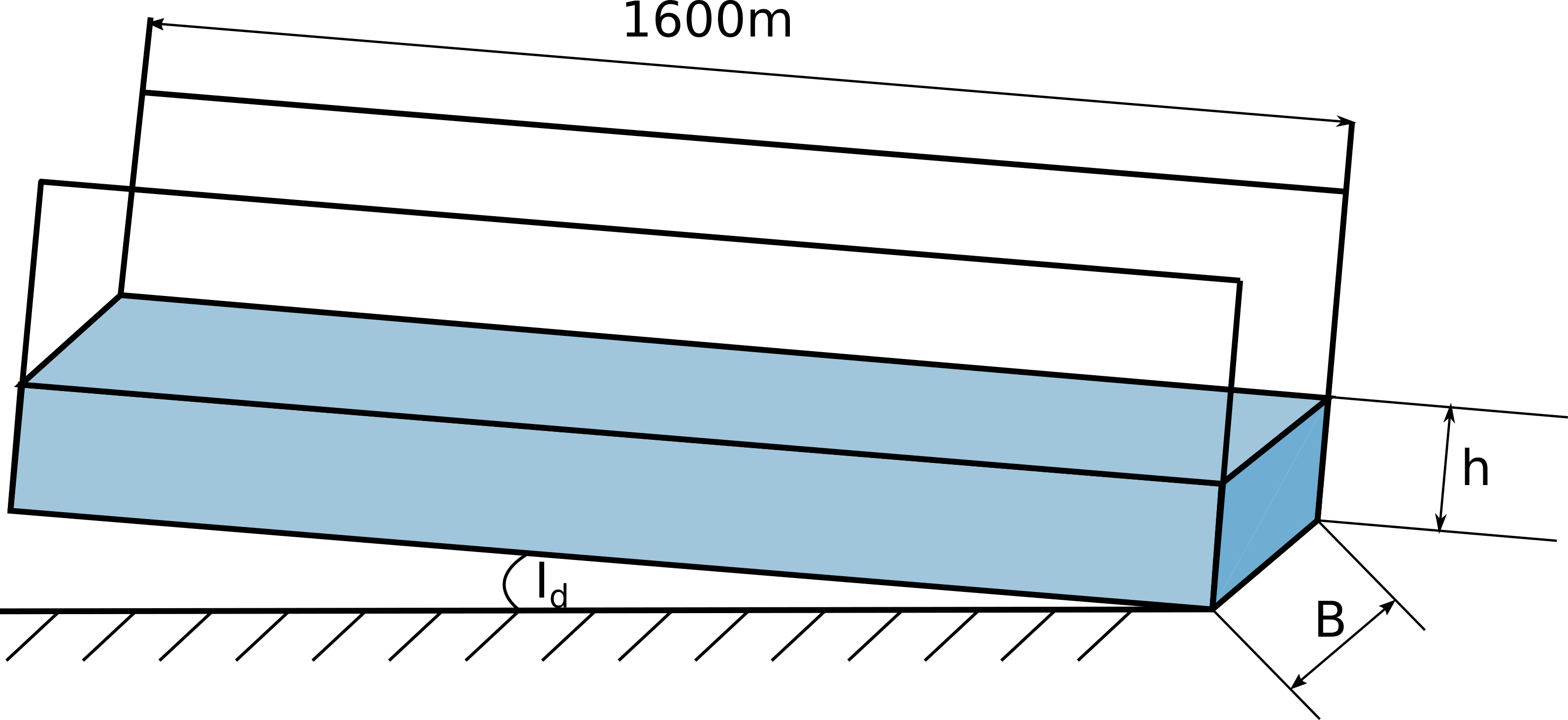
Sl. 32 Postavka problema propagacije poplavnog talasa u vremenu.

Maningova hrapavost ima vrednost od \(n = 0,015 m^{-\frac{1}{3}}s\), nagib je postavljen na \(I_d=0,005\), a brzina propagacije na \(c=15 \, m/s\). Cilj je izračunati promene dubine i protoka vode duž kanala, izazvane poplavnim talasom generisanim kao uzvodni granični uslov na \(x=0\):

\[Q_{in}(t) = Q(0,t) = 180 \cdot \left[ 1 + \left( -\frac{sgn(t-600)}{2} + \frac{1}{2} \right) \cdot \sin \left( \frac{\pi t}{600} \right) \right].\]

Pored ovog uslova, tu je i početni uslov Dirihleovog tipa, a to je da je visina vode u kanalu \(h(x,t=0)=1,751m\). Interesantni delovi rešenja prikazani su na Listing 7.

Listing 7 Rešenje problema propagacije poplavnog talasa korišćenjem DeepXDE okvira

import deepxde as dde
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from deepxde.backend import tf

c = 15 # brzina propagacije talasa
n = 0.015 # hrapavost kanala
Id = 0.005 # nagib dna kanala
B = 15 # poprecni presek
length = 1600
total_time = 1000.0

# Hiperparametri
layers = [2] + [30] * 4 + [1]
activation = 'tanh'
initializer = 'Glorot uniform'
optimizer = 'rmsprop'
batch_size = 128
num_of_epochs = 20000
learning_rate = 0.001
loss = 'mse'

# Jednacina kontinuiteta
def pde(x, h):
    dh_t = dde.grad.jacobian(h, x, i = 0, j = 1)
    dh_x = dde.grad.jacobian(h, x, i = 0, j = 0)
    return dh_t + c * dh_x

# Da li je t=0?
def initial_h(x, on_boundary):
    return on_boundary and np.isclose(x[1], 0)

# Da li je x=0?
def boundary_hx0(x, on_boundary):
    return on_boundary and np.isclose(x[0], 0)

# Pocetni uslov za visinu vode x(t=0)
def func_init_h(x):
    return 1.751

# Dirihleov granicni uslov - Profil poplavnog talasa u vremenu
def func_hx0(x):
    t = x[:, 1:2]

    Qin = 180 * (1 + (-(np.sign(t - 600) / 2) + 0.5) * np.sin(t *  np.pi / 600))
    a = Qin * n
    b = B * np.sqrt(Id)
    c = a / b
    return custom_pow(c, 3/5)

time_domain = dde.geometry.TimeDomain(0, total_time)
geom_domain = dde.geometry.Interval(0, length)
geotime = dde.geometry.GeometryXTime(geom_domain, time_domain)

# Realizacija granicnog i pocetnog uslova
bc = dde.icbc.DirichletBC(geotime, func = func_hx0, on_boundary = boundary_hx0)
ic = dde.icbc.IC(geotime, func = func_init_h, on_initial = initial_h)

# Konstrukcija modela i definisanje kolokacionih tacaka
data = dde.data.TimePDE(geotime, pde, [bc, ic], num_domain = 16000, num_boundary = 1000,
      num_initial = 100, train_distribution = 'uniform')
net = dde.nn.FNN(layers, activation, initializer)
model = dde.Model(data, net)

# Treniranje RMSProp metodom
model.compile(optimizer = optimizer, loss = loss, lr = learning_rate)
loss_history, train_state = model.train(epochs = num_of_epochs, display_every = 1000, batch_size = batch_size)

# Dodatno treniranje L-BFGS-B metodom posle RMSprop optimizacije
model.compile("L-BFGS-B")
loss_history, train_state = model.train()

U ovoj skripti odmah na početku definišemo i fizičke parametre problema i hiper-parametre modela. Pogledom na grupu hiper-parametara odmah može da se primeti značajno veći broj epoha za trening, kao i optimizator RMSProp umesto standardnog Adam optimizatora. Adam optimizator prilikom računanja gradijenta koristi i prvi i drugi izvod (moment), dok RMSProp koristi samo drugi izvod. Tokom eksperimentisanja sa različitim hiper-parametrima, ispostavilo se da za ovaj konkretan primer RMSProp zaista nešto brže konvergira. Takođe, pokazalo se da je primer u nekim scenarijima osetljiv čak i na izbor batch_size i inicijalizatora težina. Praksa je pokazala da je uz aktivacione funkcije kao što su sigmoid ili tanh bolje koristiti Glorot inicijalizator, dok uz aktivacionu funkciju relu bolje ide He, po Katanforoosh and Kunin [KK19].

Na žalost, oko izbora hiper-parametara ne postoje stroga pravila. Sve zavisi od samog primera, pa se izbor optimalnih hiper-parametara za neki konkretan problem uglavnom svodi na manuelnu, vremenski zahtevnu proceduru. Pomoću alata kao što je Tensorflow/Keras može se donekle umanjiti ovaj problem jednostavnim algoritmima kao što je nasumična pretraga (Random Grid Search), koja zahteva ogromne računarske resurse da bi se dobili iole upotrebljivi rezultati. S druge strane, postoji nekoliko alata koji ovu pretragu čine efikasnijom pametnijim pristupom optimizaciji. Na primer, alat Blackfox koristi distribuirani genetski algoritam, a problem hardverskih resursa rešava distribuiranom obukom na lokalnom Kubernetes klasteru ili klasteru postavljenom na nekom klaud provajderu.

Sledi postavka početnog Dirihleovog uslova za nivo vode u kanalu i nešto složenijeg graničnog uslova za visinu vode \(h\) koji se menja u vremenu po jednačini (29). Ovde samo treba naglasiti da se kod DeepXDE ulazi \(x\) i \(t\) zadaju kao jedan dvokolonski tenzor, u kome je:

x[:, 0:1] # ulaz x
x[:, 1:2] # ulaz t

Kako je u pitanju dinamički problem koji pokriva relativno veliki prostorni i vremenski domen, tj. prati se linija od 1,6 km tokom približno 17 minuta, potreban je i veći broj kolokacionih tačaka nego u nekim problemima koje smo ranije obrađivali. Model se postavlja kao:

data = dde.data.TimePDE(geotime, pde, [bc, ic], num_domain = 16000, num_boundary = 1000,
  num_initial = 100, train_distribution = 'uniform')

Brojnost kolokacionih tačaka za početne i granične uslove prati brojnost tačaka unutar domena. Nakon standardnog treniranja metodom RMSProp primećujemo još jednu specifičnost u odnosu na jednostavnije primere. Naime, nakon što se obavi „globalna” pretraga, algoritam Limited Memory Broyden-Fletcher-Goldfarb-Shanno ima priliku da se dodatno približi optimalnom rešenju prema Markidis [Mar21]:

model.compile("L-BFGS-B")
loss_history, train_state = model.train()

Primećujemo da se ovde ne navodi broj epoha, već se algoritam oslanja na automatsku detekciju konvergencije. Grafik funkcije gubitka se može videti na Sl. 33, gde do 20.000. epohe, kao što je već rečeno, teče RMSProp, a onda se u lokalnoj okolini nastavlja sa L-BFGS-B. Veoma je uočljiv rast performansi treniranja, tj. pad vrednosti funkcije gubitka u tom delu.

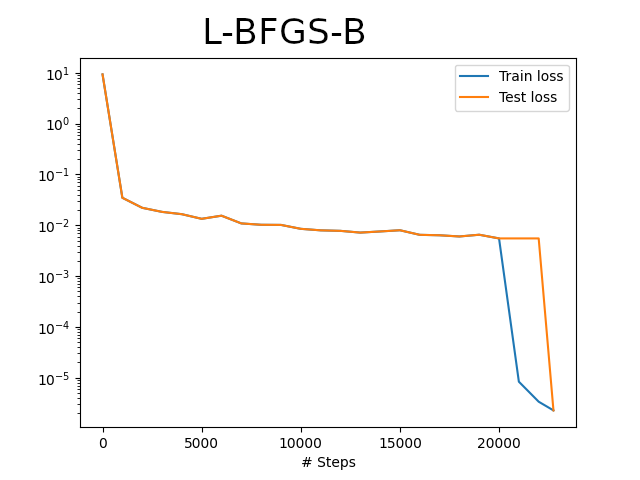
Sl. 33 Početno treniranje metodom RMSProp u 20.000 epoha i dodatno treniranje metodom L-BFGS-B do detektovane konvergencije

Što se samog procesa treniranja ove NMPFZ tiče, treba naglasiti da je za ovoliku količinu podataka, tj. kolokacionih tačaka, taj proces daleko brže radi na grafičkom procesoru nego na standardnom procesoru. Slobodna procena je da je treniranje na Tesla T4 grafičkom procesoru više od 10 puta brže nego na procesoru Intel Xeon Silver 4208 @ 2.10GHz.

Konačno dolazimo i do rezultata. Visina vodenog stuba u više kontrolnih tačaka (0, 400m, 800m, 1200m, 1600m) prikazana je na Sl. 34. Ova rešenja se dobro poklapaju sa rešenjima koje daje metoda konačnih razlika, ali to poređenje ovde nećemo prikazivati.

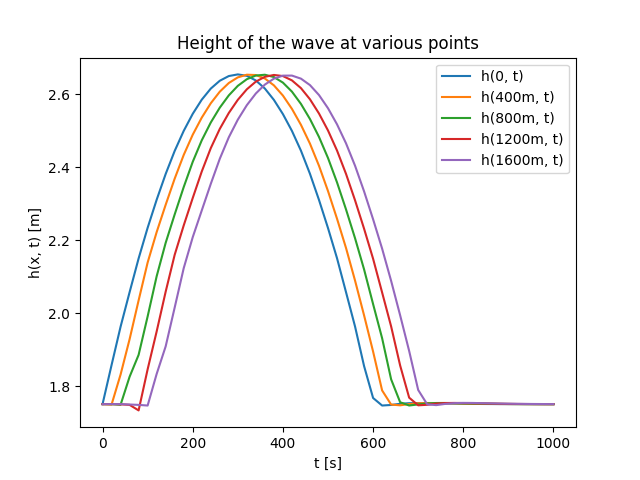
Sl. 34 Visina vodenog talasa u nekoliko tačaka tokom vremena

Inverzni problem

Pošto smo uspešno rešili direktni problem, hajde da zamislimo situaciju da nam nije poznat parametar \(n\) koji reprezentuje Maningovu hrapavost, ali da smo posmatranjem kretanja talasa utvrdili da je njegov vrh visine 2,65m prošao kroz kontrolne tačke (0, 400m, 800m, 1200m, 1600m) u sledećim trenucima:

x [m]	0	400	800	1200	1600
t [s]	300	320	360	380	400

Ove opservacije čine mogućim kreiranje PointSet graničnog uslova koji smo već koristili, a to se kod DeepXDE okvira radi na sledeći način:

bc_x = np.array([[0,300],[400,320],[800,360],[1200,380],[1600,400]]).reshape(5,2)
bc_y = np.array([2.65,2.65,2.65,2.65,2.65]).reshape(5,1)
ic3 = dde.icbc.PointSetBC(bc_x, bc_y, component=0)

Rezultati visine vodenog stuba su prikazani na Sl. 35, dok je vrednost parametra \(n\) tokom obuke prikazana na Sl. 36.

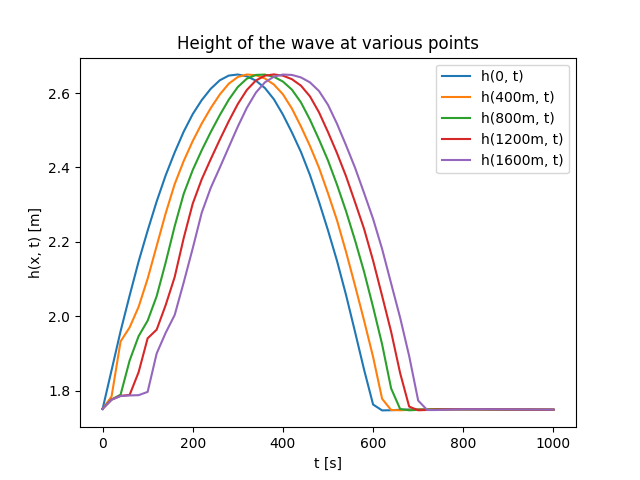
Sl. 35 Visina vodenog stuba kod inverznog problema

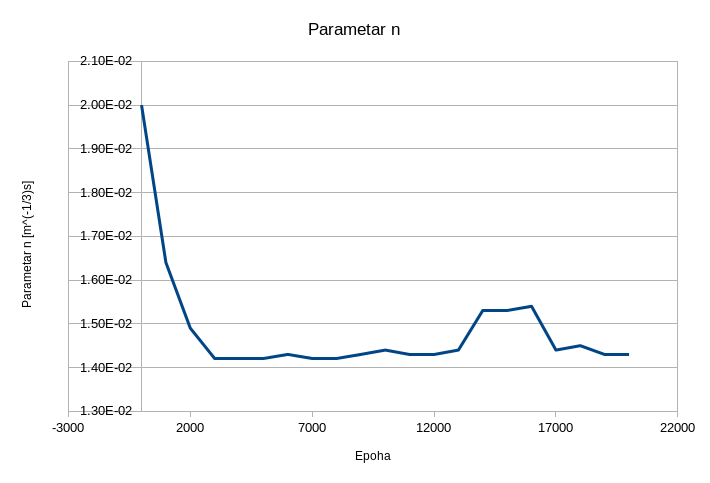
Sl. 36 Vrednost nepoznatog parametra \(n\) tokom obuke

Vidimo da se NMPFZ i u ovom problemu dosta dobro snalazi sa inverznom postavkom. Još jednom valja naglasiti da se kod NMPFZ direktni i inverzni pristup metodološki uopšte ne razlikuju i da zahtevaju istu količinu računarskih resursa. Nasuprot tome, klasične numeričke metode kao MKE su u stanju da reše isključivo direktne probleme. Za indentifikaciju parametara kod MKE moraju da se koriste metode za konveksnu ili češće, nekonveksnu optimizaciju koje su u realnim primenama računarski veoma zahtevne, a ponekad i nerešive.

Naravno, ni NMPFZ nije idealan. Uspešnost obuke i ovom primeru mnogo zavisi od izbora hiper-parametara, a često se dešava da usled stohastičkog karaktera same obuke ni isti hiper-parametri ne dovode do rešenja baš u svakom treningu. Pored hiper-parametara, ovde imamo i početnu vrednost nepoznatog fizičkog parametra (ili više parametara), pa se neretko dešava da optimizacija za neke početne vrednosti uopšte ne konvergira, zadržavajući se u nekom lokalnom minimumu.