Oscilator

Jedno od najjednostavnijih periodičnih kretanja u mehanici je oscilatorno kretanje (oscilovanje), gde se telo kreće po istoj putanji, ali menja smer kretanja. Ako bismo razmatrali oscilatorno kretanje u idealnim uslovima, bez trenja i otpora sredine, ono bi trajalo beskonačno dugo. Pri takvim slobodnim, neprigušenim oscilacijama, oscilator ne gubi energiju, a amplituda se ne menja u toku vremena. Međutim, u realnim uslovima, mora da se uzme u obzir uticaj okoline na kretanje tela. Oscilovanje usporava sa vremenom, smanjuju se amplitude, jer se ukupna mehanička energija troši na savladavanje otpora sredine. To su tzv. prigušene oscilacije, kada oscilator gubi energiju i amplituda se smanjuje u toku vremena. Treći slučaj bi bio kada gubitak energije oscilatora može da se nadoknadi delovanjem spoljašnje periodične sile. Amplituda oscilovanja će pri ovakvom načinu kretanja ostati konstantna, ukoliko se pri svakom ciklusu kretanja u sistem doda energija jednaka onoj energiji koju je sistem izgubio. Ovakvo kretanje se naziva prinudno oscilovanje.

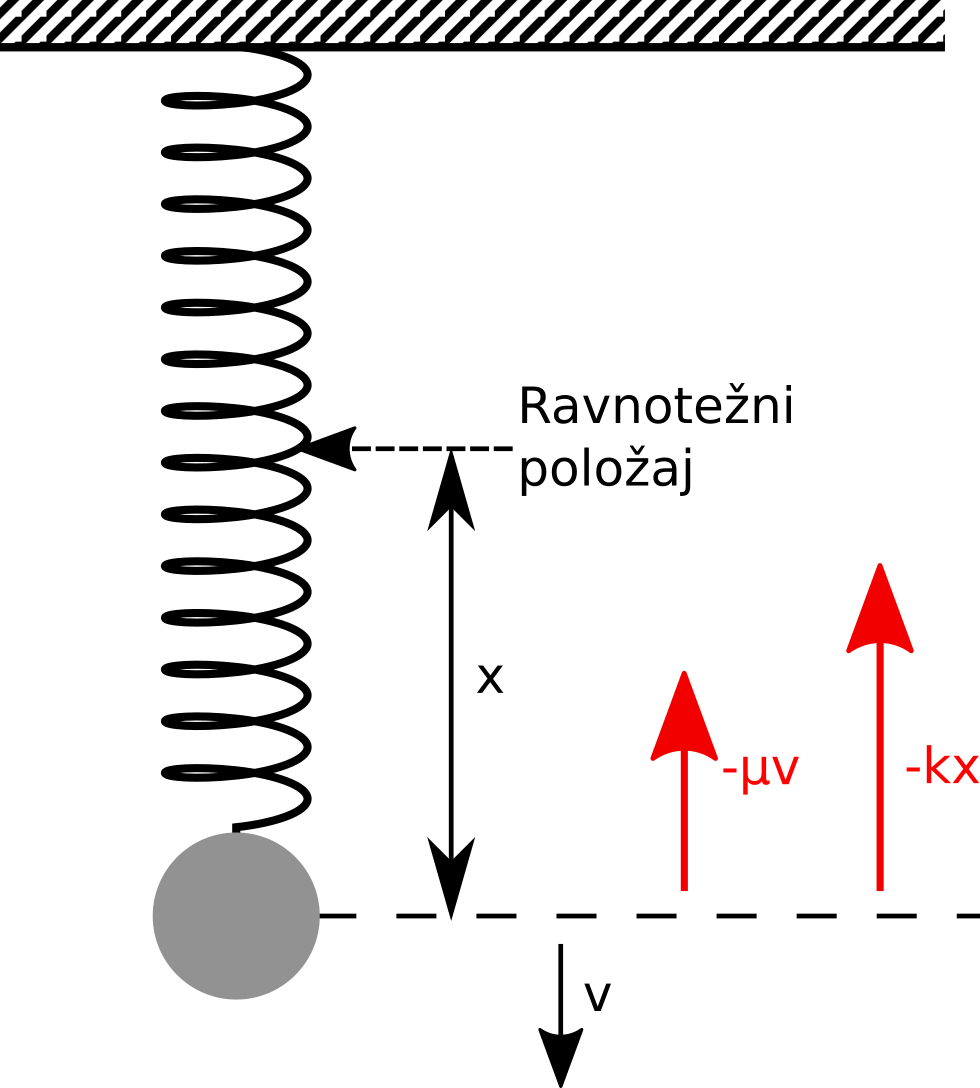
Sl. 15 Postavka eksperimenta sa oprugom i tegom. Na teg deluju sila elastičnosti opruge i sila trenja.

Problem koji rešavamo predstavlja modelovanje oscilovanja tega koji visi na opruzi, kao što je prikazano na Sl. 15. Parametri koji utiču na kretanje su masa tega, koeficijent trenja i koeficijent elastičnosti opruge. Sile koje utiču na kretanje oscilatora su:

• Povratna sila opruge \(F_f = k \cdot x\) vuče teg ka tački mirovanja i direktno je proporcionalna otklonu klatna. Njen smer je suprotan od smera otklona. Parametar \(k\) predstavlja konstantu opruge.

• Sila trenja \(F_r = -\mu \cdot \dot{x}\) je proporcionalna brzini tega, dok je smer uvek suprotan smeru kretanja tega. Parametar \(\mu\) predstavlja koeficijent trenja.

Dakle, sila inercije je suprotstavljena dvema silama:

\[m \ddot{x} = -\mu \dot{x} - k x\]

ili transformisano:

(20)\[\ddot{x} + \frac{\mu}{m} \dot{x} + \frac{k}{m} x = 0\]

Ova jednačina je linearna homogena diferencijalna jednačina drugog reda sa konstantnim koeficijentima. Za analitičko rešavanje diferencijalne jednačine ovog tipa koristi se eksponencijalna funkcija oblika:

\[x(t) = C e^{\lambda t}\]

Prvi i drugi izvod ove jednačine glase:

(21)\[\dot{x}(t) = \lambda C e^{\lambda t}, \qquad \ddot{x}(t) = \lambda^2 C e^{\lambda t}\]

Zamenom jednačina (21) u diferencijalnu jednačinu (20) i skraćivanjem dobijamo:

(22)\[\lambda^2 + \frac{\mu}{m} \lambda + \frac{k}{m} = 0\]

Ova jednačina se naziva karakterističnom jednačinom. Kako je u pitanju kvadratna jednačina, razmatramo dva rešenja:

\[\lambda_{1,2} = -\frac{\mu}{2m} \pm \sqrt{\left(\frac{\mu}{2m}\right)^2-\frac{k}{m}}.\]

Da bismo dodatno uprostili izraz, uvodimo nove konstante \(\delta\) i \(\omega_0\):

\[\delta=\frac{\mu}{2m}, \qquad \omega_0=\sqrt{\frac{k}{m}},\]

pa se rešenja karakteristične jednačine mogu izraziti u obliku:

(23)\[\lambda_{1,2} = -\delta \pm \sqrt{\delta^2-\omega_0^2}.\]

U zavisnosti od izbora konstanti \(\delta\) i \(\omega_0\), diskriminanta može biti: veća od nule, manja od nule ili jednaka nuli. Stoga \(\lambda_1\) i \(\lambda_2\) mogu biti:

• dva realna različita rešenja,

• dva konjugovano kompleksna rešenja i

• dva jednaka realna rešenja.

Svaki od ovih slučajeva zahteva drugačiji pristup analitičkom rešavanju. Uopšteno rešenje homogene jednačine ima oblik:

(24)\[x(t) = C_1 \cdot x_1(t) + C_2 \cdot x_2(t),\]

gde funkcije \(x_1(t)\) i \(x_2(t)\) zavise od vrednosti determinante u jednačini (23). Sada ćemo razmotriti sve navedene slučajeve.

Preprigušeni slučaj

Ukoliko je \(\delta > \omega_0\), onda dominira sila trenja. Stoga je diskriminanta u jednačini (23) pozitivna i postoje dva različita realna rešenja \(\lambda_1 \ne \lambda_2\):

\[x_1(t)=C_1 e^{\lambda_1 t}, \qquad x_2(t)=C_2 e^{\lambda_2 t}.\]

Zamenom u jednačinu (24) dobijamo opšte rešenje diferencijalne jednačine:

\[x(t) = C_1 e^{\left(-\delta+\sqrt{\delta^2-\omega_0^2}\right) t} + C_2 e^{\left(-\delta-\sqrt{\delta^2-\omega_0^2}\right) t}.\]

Uslov koji smo naveli za preprigušeni slučaj nalaže da je

\[\delta > \sqrt{\delta^2-\omega_0^2},\]

pa je stoga rešenje zbir dveju eksponencijalnih opadajućih funkcija. Kako bismo dalje uprostili izraz, zamenićemo koren novom konstantom:

\[\alpha = \sqrt{\delta^2-\omega_0^2},\]

pa konačno rešenje za preprigušeni slučaj glasi:

\[x(t) = e^{-\delta t} \left(C_1 e^{\alpha t} + C_2 e^{-\alpha t}\right).\]

Integracione konstante \(C_1\) i \(C_2\) možemo dobiti iz početnih uslova, tj. početnog položaja i početne brzine tega:

\[x(0)=x_0, \quad \dot{x}(0)=v_0.\]

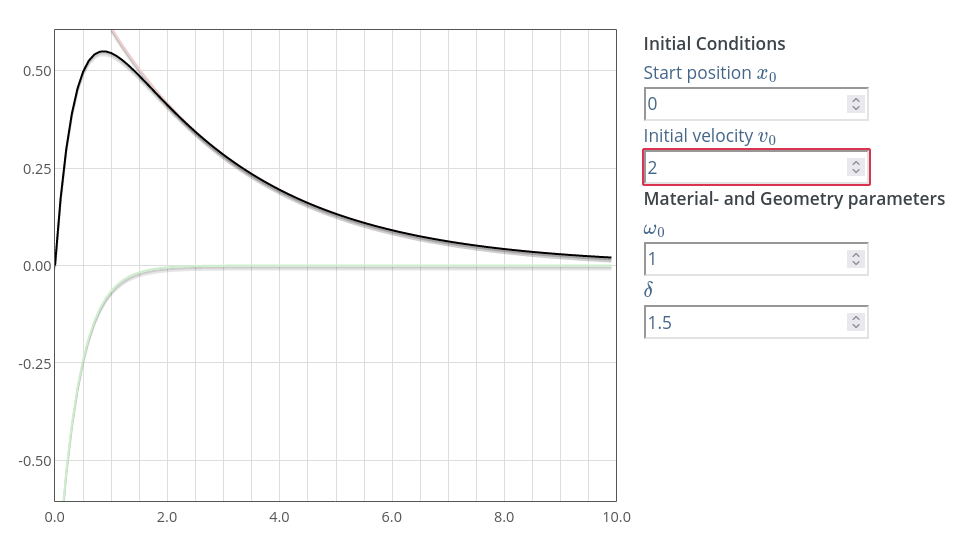
Sl. 16 Promena položaja tega u toku vremena za preprigušeni slučaj oscilovanja. Dobijeno pomoću simulatora.

Na Sl. 16 možemo videti grafički prikaz opšteg analitičkog rešenja za preprigušeni slučaj oscilatora. Ovaj dijagram prikazuje kretanje tega tokom vremena. Crvena linija označava komponentu rešenja \(C_1 e^{\lambda_1 t}\), dok zelena označava drugu komponentu rešenja \(C_2 e^{\lambda_1 t}\). Crna linija je zbir ova dva parcijalna rešenja i predstavlja ukupno rešenje diferencijalne jednačine preprigušenog slučaja za zadate početne uslove.

Kritično-prigušeni slučaj

Ovaj slučaj se dešava kada je \(\delta=\omega_0\). U ovom slučaju jednačina (23) ima samo jedno rešenje

\[\lambda=\lambda_1=\lambda_2=-\delta\]

Dve komponente rešenja diferencijalne jednačine su onda:

\[x_1(t)=C_1 e^{\lambda t}, \qquad x_2(t) = t C_2 e^{\lambda t}.\]

Zamenom ovih izraza u opšte rešenje (24) dobijamo:

\[x(t) = e^{-\delta t} (C_1 + t C_2)\]

Integracione konstante \(C_1\) i \(C_2\) možemo dobiti iz početnih uslova, tj. početnog položaja i početne brzine tega.

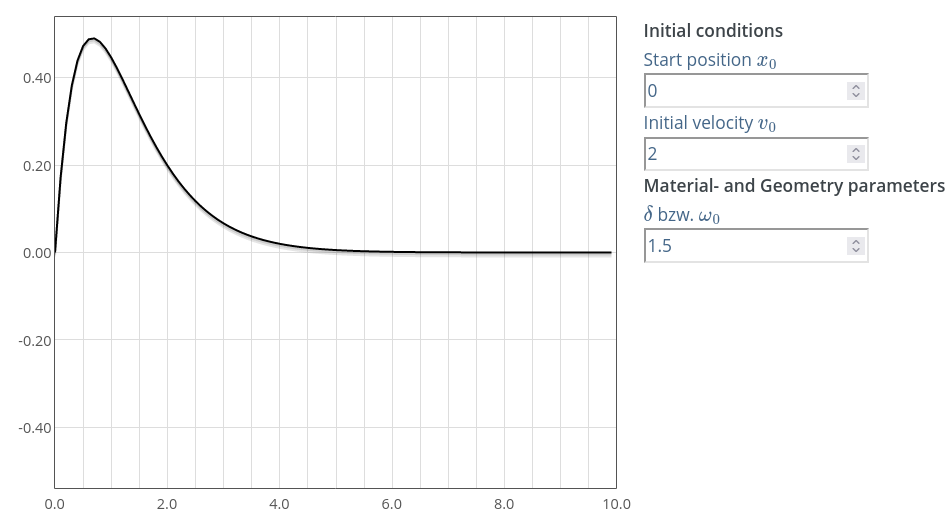
Sl. 17 Promena položaja tega u toku vremena za kritično prigušeni slučaj oscilovanja. Dobijeno pomoću simulatora.

Na Sl. 17 vidimo grafički prikaz opšteg rešenja kritično prigušenog slučaja. Na dijagramu opažamo kretanje klatna tokom vremena za zadate početne uslove.

Podprigušeni slučaj

Podprigušeni slučaj nastupa kada je \(\delta < \omega_0\), tj. diskriminanta jednačine (23) je negativna. Stoga su \(\lambda_1\) i \(\lambda_2\) kompleksni brojevi. Eksponencijalni izraz

\[x(t) = C e^{\lambda t}\]

se ponovo koristi za dobijanje komponenti rešenja ove diferencijalne jednačine:

\[x_1(t)=C_1 e^{\lambda_1 t}, \qquad x_2(t) = C_2 e^{\lambda_2 t}.\]

Zamenom u izraz (24) i zamenom \(\lambda\) dobijamo:

(25)\[x(t) = e^{-\delta t} \left( C_1 e^{\sqrt{\delta^2-\omega_0^2} t} + C_2 e^{-\sqrt{\delta^2-\omega_0^2} t} \right).\]

Sada radimo sa kompleksnim rešenjima jer su vrednosti negativne. Stoga konstante \(C_1\) i \(C_2\) imaju kompleksne vrednosti. Za rad sa kompleksnim vrednostima koristimo Ojlerovu formulu:

\[e^{i\phi} = \cos\phi + i\sin\phi\]

Korisno bi bilo da izmenimo jednačinu tako što bismo razdvojili imaginarne delove:

\[\sqrt{\delta^2-\omega_0^2} = \sqrt{-1 \cdot (\omega_0^2-\delta^2)} = i \sqrt{\omega_0^2-\delta^2}.\]

Dobijamo deo koji se sastoji od imaginarne vrednosti \(i\) pomnoženom korenom realnih vrednosti. Da bismo uprostili dalja izračunavanja, zamenjujemo koren novom konstantom

\[\omega = \sqrt{\omega_0^2-\delta^2}\]

Ova konstanta predstavlja prirodnu frekvenciju harmonijskog oscilatora. Tada jednačina (25) može da se transformiše u:

\[x(t) = e^{-\delta t} \left( C_1 e^{i\omega t} + C_2 e^{-i\omega t} \right).\]

Sa fizičke strane, interesuju nas samo realne vrednosti. Da bismo ih pronašli, neophodno je da razdvojimo imaginarni i realni deo. Kao što je već pomenuto, konstante \(C_1\) i \(C_2\) su konstante sa kompleksnim vrednostima, a njihov polarni oblik je:

\[C_1 = \hat{C_1}e^{i\phi_1}, \qquad C_2 = \hat{C_2}e^{i\phi_2}\]

Kako analitičko rešavanje ovog problema nije u fokusu ovog materijala, nećemo do kraja analitički izvoditi izraz, već samo navesti krajnje rešenje za podprigušeni slučaj, nakon odabira realnih rešenja i transformacije i odabira odgovarajućih konstanti:

\[x(t) = e^{-\delta t} (2A\cos(\phi+\omega t))\]

\(A\) je amplituda, a \(\phi\) je fazni pomeraj. Konstante se mogu dobiti iz početnih uslova, kao što su:

\[x(0)=x_0, \quad \dot{x}(0)=v_0.\]

Ovim smo izveli sva potrebna analitička rešenja sa kojima ćemo porediti rešenje dobijeno pomoću NMPFZ pristupa.

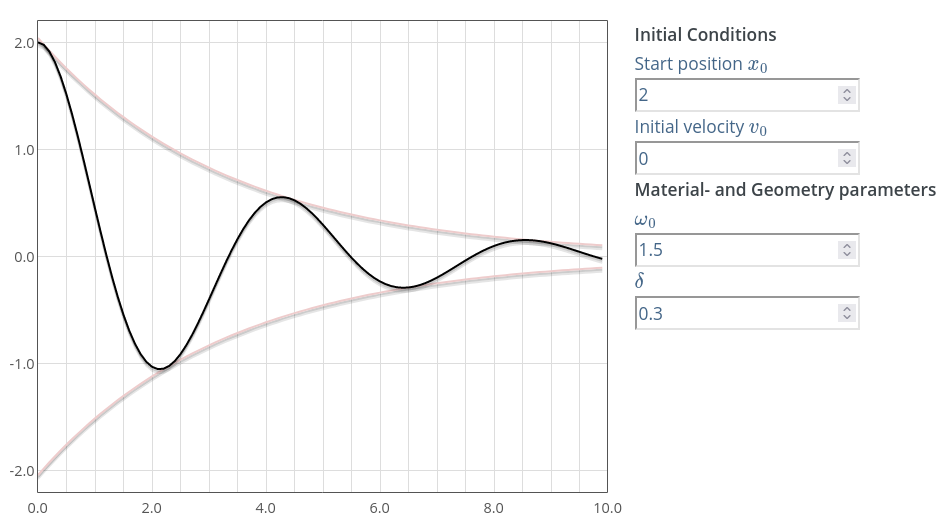
Sl. 18 Promena položaja tega u toku vremena za podprigušeni slučaj oscilovanja. Dobijeno pomoću simulatora.