Rešenja direktnog problema

Sada ćemo se pozabaviti rezultatima procesa učenja koji smo uspostavili u prethodnoj sekciji Implementacija.

Podprigušeni slučaj

Za slučaj da je:

\[\begin{split}m = 1 \\ \mu = 0,1 \\ k = 2\end{split}\]

imamo da su:

\[\begin{split}\delta = \frac{\mu}{2m} = 0,05 \\ \omega_0 = \sqrt{\frac{k}{m}} = \sqrt{2}\end{split}\]

Kako je \(\delta^2-\omega_0^2 < 0\), imaćemo dva konjugovano-kompleksna rešenja, tj. podprigušeni slučaj opisan u sekciji Podprigušeni slučaj. Rešenja dobijena skriptom datom u Implementacija, gde su početni uslovi postavljeni tako da je \((x_0=0, v_0=2)\) prikazana su na Sl. 19.

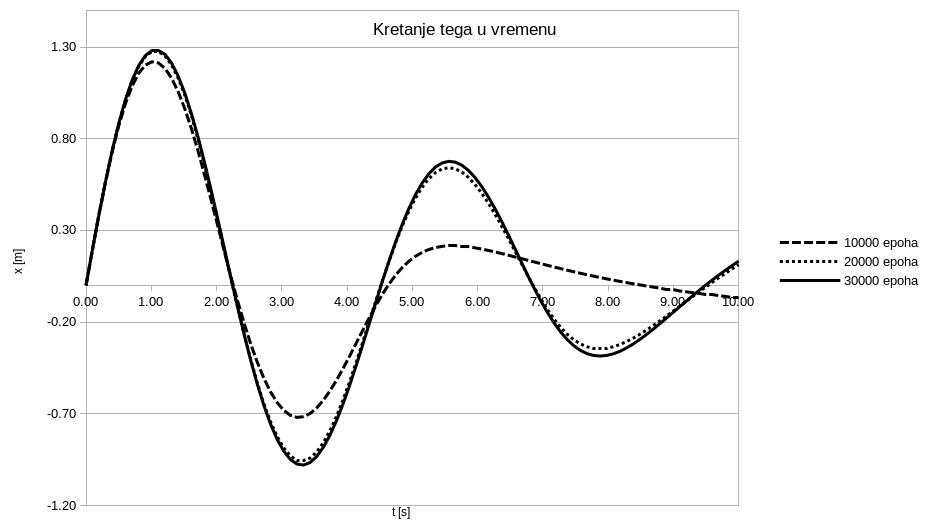
Sl. 19 NMPFZ rešenje promene položaja tega u toku vremena za podprigušeni slučaj oscilovanja.

Na grafiku se može videti kako se rezultati razlikuju u odnosu na to koliko epoha je mreža trenirana. Naime, rezultati za 10000 epoha su značajno lošiji nego oni za 20000 i 30000 epoha. Dakle, kao i kod gotovo svih problema dubokog učenja i kod NMPFZ taj proces treba pratiti (Sl. 20) i trening prekinuti tek kada je dosegnut odgovarajući minimum i učenje dalje ne napreduje značajno.

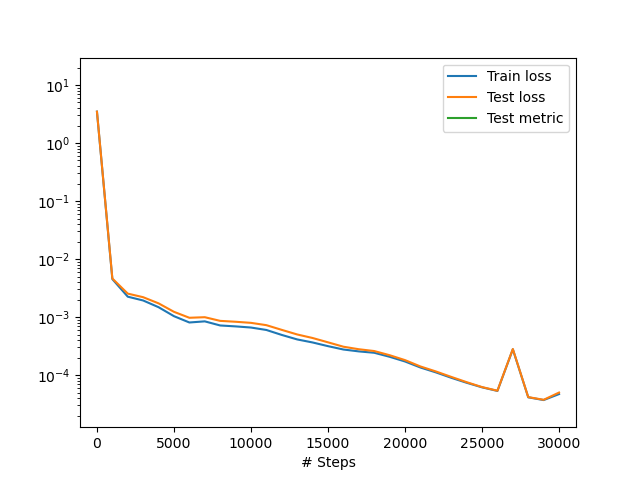
Sl. 20 Funkcija gubitka u toku procesa učenja.

Preprigušeni slučaj

Ukoliko je, na primer:

\[\begin{split}m = 1 \\ \mu = 3 \\ k = 1\end{split}\]

imamo da su:

\[\begin{split}\delta = \frac{\mu}{2m} = 1,5 \\ \omega_0 = \sqrt{\frac{k}{m}} = 1\end{split}\]

Kako je \(\delta^2-\omega_0^2 > 0\), imaćemo dva različita realna rešenja, tj. preprigušeni slučaj opisan u sekciji Preprigušeni slučaj. Rešenja dobijena skriptom datom u Implementacija za početne uslove \((x_0=0, v_0=2)\) prikazana su na Sl. 21.

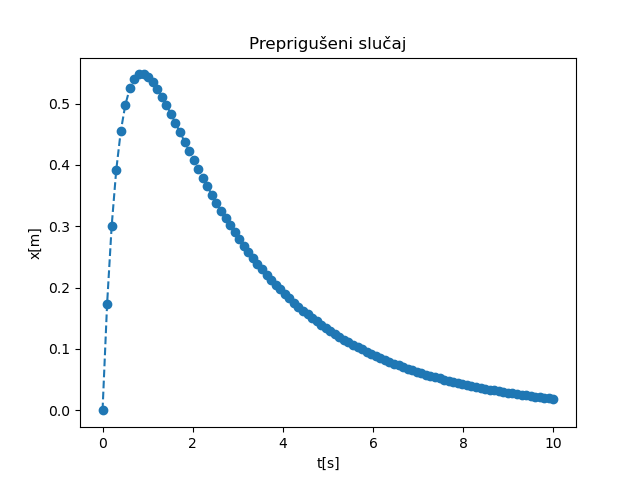
Sl. 21 NMPFZ rešenje promene položaja tega u toku vremena za preprigušeni slučaj oscilovanja.

Kritično-prigušeni slučaj

Preostao je još kritično-prigušeni slučaj, koji će se dobiti ukoliko postavimo sledeće parametre problema:

\[\begin{split}m = 1 \\ \mu = 3 \\ k = 2,25\end{split}\]

Imamo da su:

\[\begin{split}\delta = \frac{\mu}{2m} = 1,5 \\ \omega_0 = \sqrt{\frac{k}{m}} = 1,5\end{split}\]

Kako je \(\delta^2-\omega_0^2 = 0\), imaćemo dva jednaka realna rešenja, tj. kritično-prigušeni slučaj opisan u sekciji Kritično-prigušeni slučaj. Rešenja dobijena skriptom datom u Implementacija za početne uslove \((x_0=0, v_0=2)\) prikazana su na Sl. 22.

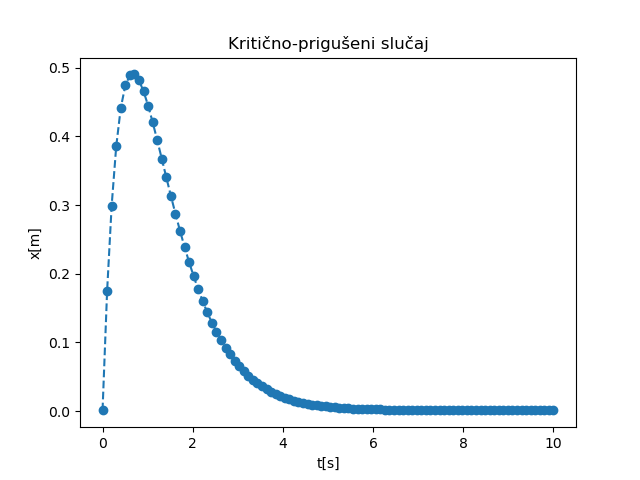
Sl. 22 NMPFZ rešenje promene položaja tega u toku vremena za kritično-prigušeni slučaj oscilovanja.