Primer konstrukcije funkcije gubitka

Rezonovanje iz prethodnog odeljka Neuronske mreže podržane fizičkim zakonima ćemo potkrepiti jednostavnim primerom. Započnimo prvo tako što ćemo uzeti neku jednostavnu diferencijalnu jednačinu. Izabraćemo logističku jednačinu (Logistic Equation) koja predstavlja model rasta populacije. Ta jednačina glasi:

(4)\[\frac{df}{dt} = R \cdot t(1-t)\]

Funkcija \(f(t)\) predstavlja stopu rasta populacije tokom vremena \(t\), dok parametar \(R\) određuje maksimalnu stopu rasta. Kako bismo od familije krivih koje zadovoljavaju rešenje ove obične diferencijalne jednačine izabrali jednu krivu kao rešenje, moramo postaviti granični, tj. početni uslov. Neka to bude:

(5)\[f(t=0) = \frac{1}{2}.\]

Kako je analitičko rešenje ove jednačine poznato, poređenjem sa njim možemo proveriti tačnost NMPFZ. Time ćemo početi da razotkrivamo potencijal primene i na kompleksnije obične i parcijalne diferencijalne jednačine. Da se podsetimo, NMPFZ su zasnovane na dve fundamentalne osobine neuronskih mreža:

• Formalno je pokazano da su neuronske mreže univerzalne funkcije aproksimacije, tako da neuronska mreža može da aproksimira bilo koju funkciju, a samim tim i rešenje za našu logističku jednačinu.

• Jednostavno je i jeftino izračunati izvode bilo kog reda izlaza iz neuronske mreže za bilo koji dati ulaz korišćenjem automatske diferencijacije.

Dakle, kao što je rečeno, možemo da konstruišemo funkciju gubitka tako da, kada se minimizuje, diferencijalna jednačine bude zadovoljena:

(6)\[\mathcal{L}_{r} = \frac{df_{NN}(t)}{dt} - R \cdot t(1-t) = 0,\]

gde je \(f_{NN}(t)\) izlaz neuronske mreže sa jednim ulazom čiji se izvod izračunava automatskim diferenciranjem. Odmah vidimo da, ukoliko izlaz iz mreže zadovoljava (6), zapravo se ta jednačina rešava. Da bi se izračunao stvarni doprinos funkciji gubitka koji se dobija iz diferencijalne jednačine, potrebno je specificirati skup tzv. kolokacionih tačaka u domenu problema i proceniti srednju kvadratnu grešku (Mean Squared Error - MSE) ili neku drugu funkciju gubitka:

(7)\[\mathcal{L}_{r} = \frac{1}{N_{r}}\sum_{i = 1}^{N_{r}} \left( \left. \frac{df_{NN}}{dt} \right|_{t_i} - R t_j (1-t_i) \right)^2,\]

gde je \(N_{r}\) broj kolokacionih tačaka \(t_j\) u kojima se računa funkcija gubitka. Gubitak zasnovan samo na rezidualima ne osigurava jedinstveno rešenje, pa stoga uključujemo i granični uslov, tako što ga dodajemo funkciji gubitka na isti način kao u jednačini (7):

(8)\[\mathcal{L}_{0} = \frac{1}{N_{0}}\sum_{i = 1}^{N_{0}} \left( \left. f_{NN}(t) \right|_{t_i} - \frac12 \right)^2, \qquad t_i \approx 0.\]

Sada imamo oba elementa da definišemo ukupnu funkciju gubitka \(\mathcal{L}\):

(9)\[\mathcal{L} = \mathcal{L}_{r} + \mathcal{L}_{0}.\]

Tokom treniranja neuronske mreže, gornji izraz se minimizuje i izlaz iz mreže trenira da zadovolji diferencijalnu jednačinu i zadat granični uslov, čime se aproksimira konačno, jedinstveno rešenje diferencijalne jednačine. Koncept NMPFZ je veoma jednostavan, i koristeći ideju opisanu u prethodnom tekstu, možemo dodati više graničnih uslova, dodati kompleksnije ili rešavati vremenski zavisne višedimenzionalne probleme koristeći mrežu sa višestrukim ulazima.

Rešenje naše logističke jednačine je dobro poznata sigmoidna funkcija prikazana na Sl. 2.

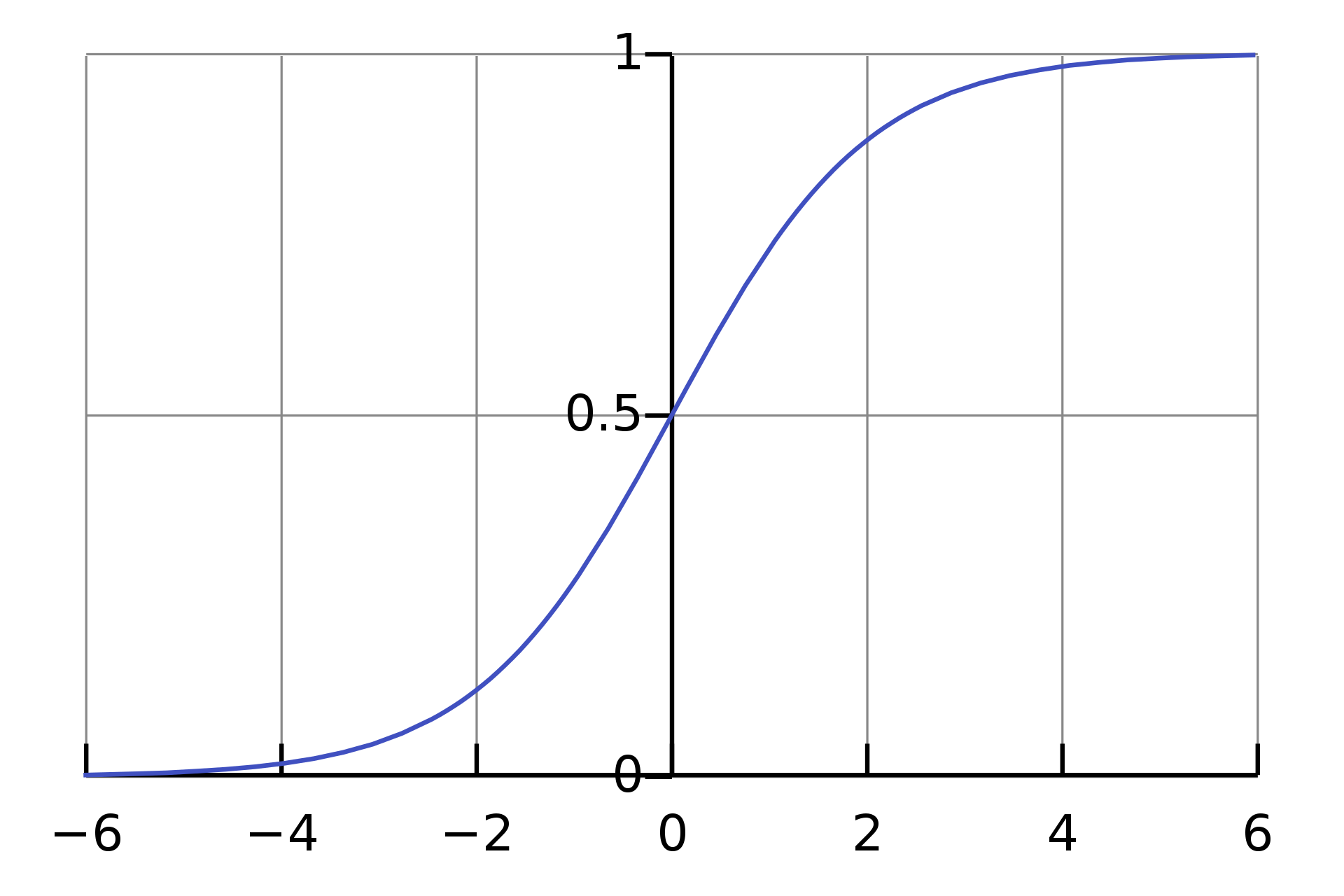
Sl. 2 Sigmoidna funkcija koja se dobija kao rešenje jednačine (4) sa početnim uslovom (5)

Način izlaganja primera

Izlaganje ćemo nastaviti konkretnim primerima. Svako poglavlje praktikuma (Provođenje toplote, Oscilacije, …) bavi se posebnom fenomenologijom i sadrži po jedan ili više direktnih ili inverznih rešenih problema. Svaki primer je potkrepljen teorijskom pozadinom, pripadajućim programskim kodom koji implementira NMPFZ rešenje, kao i analizom tačnosti i efikasnosti NMPFZ rešenja u odnosu na analitička rešenja, ukoliko postoje, ili rešenja dobijena klasičnim numeričkim metodama.

Valja napomenuti da primeri nisu sortirani po težini, već isključivo po fenomenologiji koja se modeluje. Ako ipak treba da preporučimo čitaocu odakle da krene sa praktičnim radom, recimo da Mehaničke oscilacije i Jednodimenzioni direktni problem predstavljaju dobru osnovu.