Jednodimenzioni direktni problem

Tanak štap od homogenog materijala je okružen izolacijom, tako da se promene temperature u štapu dešavaju samo kao posledica razmene toplote ka krajevima štapa i provođenja toplote duž štapa. Štap je jedinične dužine. Oba kraja su izložena mešavini vode i leda temperature 0. Početna temperatura na rastojanju \(x\) od levog kraja štapa je \(sin{(\pi x)}\), kao što se vidi na Sl. 3.

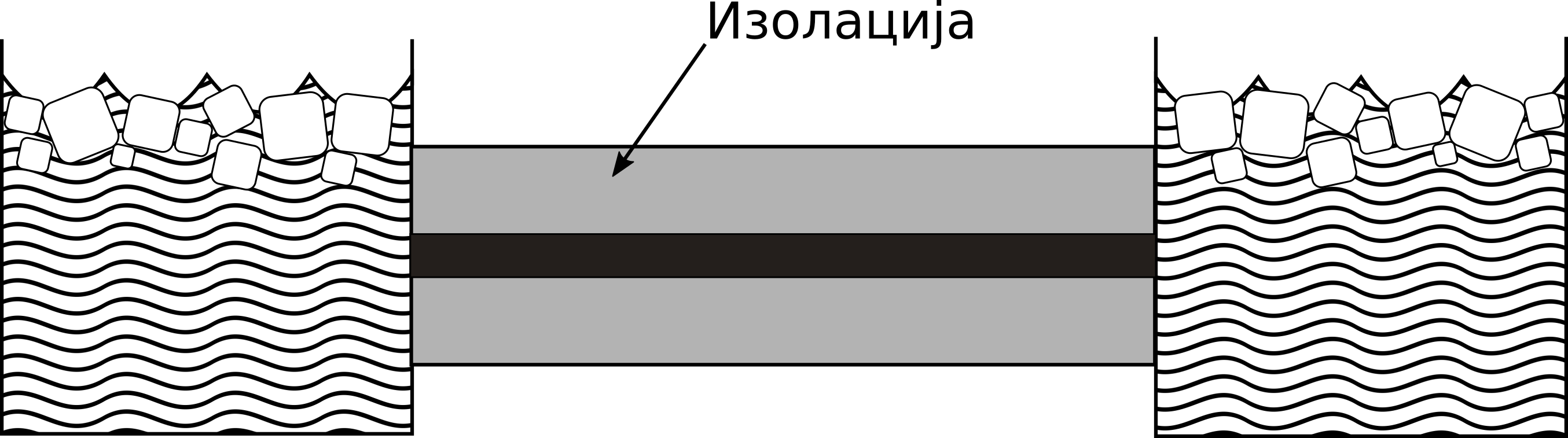
../_images/fdheat.png

Sl. 3 Eksperimentalna postavka problema provođenja toplote duž štapa. Na krajevima štapa nalazi se mešavina vode i leda. Štap je izolovan od uticaja spoljašnje sredine.

Radi poređenja, pokazaćemo sada kako se ovaj relativno jednostavan problem formuliše pomoću klasične metode konačnih razlika, a zatim ćemo rešiti direktni i inverzni problem opisane postavke NMPFZ metodom.

Rešavanje metodom konačnih razlika (MKR)

Parcijalna diferencijalna jednačina (10) modeluje temperaturu u bilo kojoj tački štapa u bilo kom vremenskom trenutku prema Recktenwald [Rec04]. Ova jednačina se rešava metodom konačnih razlika, koja daje aproksimaciju rešenja za raspored temperature, primenjujući prostornu i vremensku diskretizaciju. Programska implementacija rešenja čuva temperaturu svake tačke diskretizacije u dvodimenzionoj matrici. Svaki red sadrži temperaturnu distribuciju štapa u nekom trenutku vremena. Štap je podeljen na \(n\) delova dužine \(h\), pa stoga svaki red ima \(n+1\) elemenata. Načelno, što je veće \(n\), manja je greška aproksimacije. Vreme od 0 do \(T\) je podeljeno u \(m\) diskretnih intervala dužine \(k\), pa stoga matrica ima \(m+1\) redova, kao što je prikazano na Sl. 5.

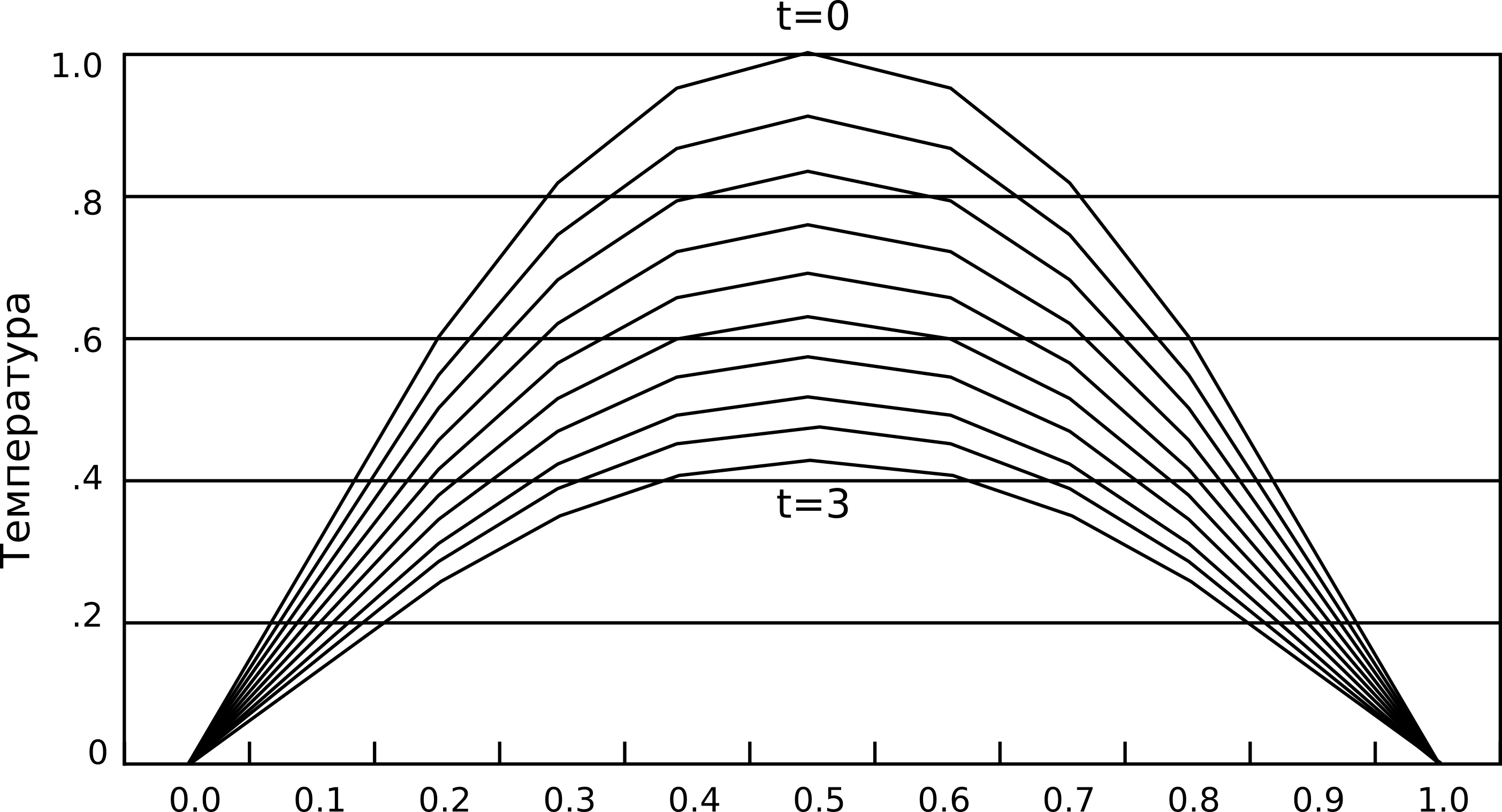
../_images/fdheat1.png

Sl. 4 Kako vreme teče, štap se hladi. Metoda konačnih razlika omogućava izračunavanje temperature u fiksnom broju tačaka u ravnomernim vremenskim intervalima. Smanjenje prostornog i vremenskog koraka uglavnom dovodi do preciznijeg rešenja.

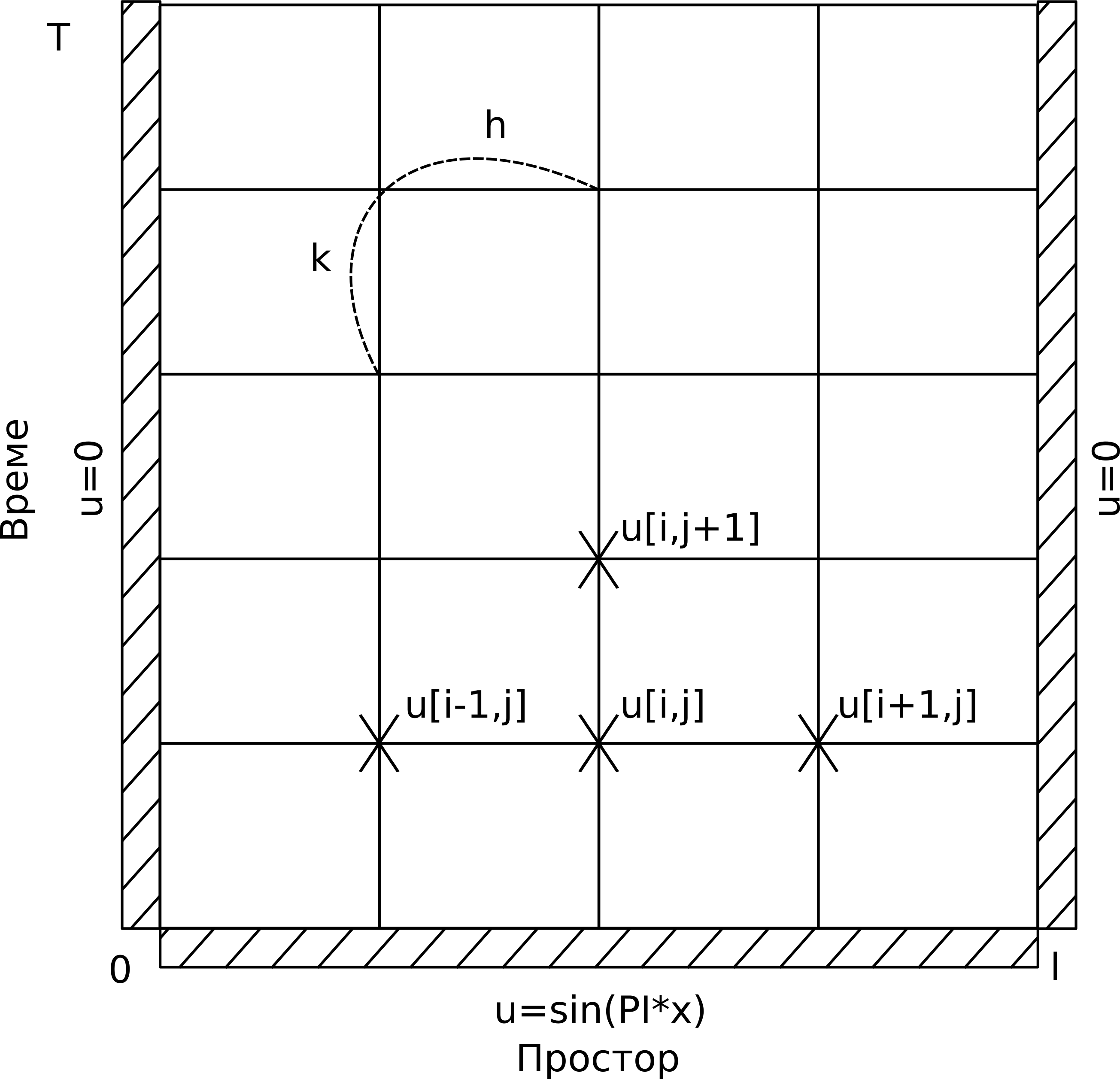
../_images/fdheat2.png

Sl. 5 Diskretizacija jednačine provođenja toplote metodom konačnih razlika

Svaka tačka \(u_{i,j}\) predstavlja element matrice koji sadrži temperaturu na poziciji \(i \cdot h\), u trenutku \(j \cdot k\). Na krajevima štapa je temperatura uvek nula. U početnom trenutku, temperatura u tački \(x\) je, kao što je već rečeno, \(sin{(\pi x)}\). Algoritam ide korak po korak kroz vreme, koristi vrednosti iz trenutka \(j\) da bi izračunao vrednosti u trenutku \(j+1\). Formula koja reprezentuje varijantu aproksimacije FTCS (Forward Time Centered Space) kao u Recktenwald [Rec04] se ovde daje bez izvođenja i glasi:

(11)\[u_{i,j+1} = R \cdot u_{i-1,j}+(1-2R) \cdot u_{i,j} + R \cdot u_{i+1,j},\]

gde je

\[R = \alpha \frac{k}{h^2}.\]

Celokupna analiza različitih eksplicitnih i implicitnih metoda data je u pomenutoj referenci, a ključni deo koda u programskom jeziku Pajton implementiran je na sledeći način:

 1 def heatFTCS(nt=10, nx=20, alpha=0.3, L=1, tmax=0.1):
 2     h = L / (nx - 1)
 3     k = tmax / (nt - 1)
 4     r = alpha * k / h**2
 5
 6     x = np.linspace(0, L, nx)
 7     t = np.linspace(0, tmax, nt)
 8     U = np.zeros((nx, nt))
 9
10     # Početni uslov
11     U[:, 0] = np.sin(np.pi * x / L)
12
13     # Glavna petlja za MKR
14     for m in range(1, nt):
15         for i in range(1, nx-1):
16             U[i, m] = r * U[i - 1, m - 1] + (1-2*r) * U[i, m-1] + r * U[i+1, m-1]
17
18     # Egzaktno rešenje za poređenje
19     ue = np.sin(np.pi * x / L) * \
20         np.exp(-t[nt - 1] * alpha * (np.pi / L) * (np.pi / L))

Kao što detaljno objašnjava Recktenwald [Rec04], ako se MKR petlja formuliše eksplicitno kao što je to slučaj kod FTCS tehnike, mora se pažljivo izabrati vremenski i prostorni korak, kako bi numerička propagacija bila „brža” od fizičke. Rešenje koje se dobija pomoću MKR šeme se može videti na Sl. 6.

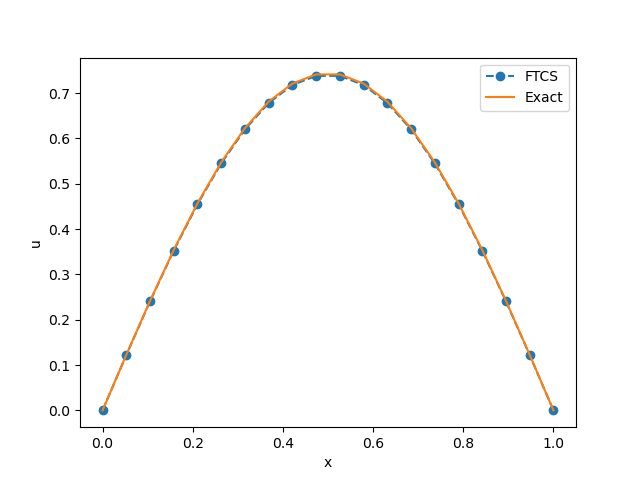
../_images/ftcs.png

Sl. 6 Rešenje koje se dobija MKR metodom koristeći eksplicitnu FTCS tehniku u trenutku \(t=0.1s\)

Ovaj problem ima i analitičko rešenje, pa je pogodan za testiranje različitih numeričkih metoda. To rešenje glasi:

(12)\[u(x,t) = \sin\left(\frac{\pi x}{L}\right) \cdot e^{-\frac{\alpha\pi^2}{L^2}t}.\]

ili u našem slučaju, kada je \(L=1\):

\[u(x,t) = \sin(\pi x) \cdot e^{-\alpha \pi^2 t}.\]

Eksplicitne tehnike poput FTCS ne garantuju konzistentnost rešenja koju garantuju implicitne tehnike kao što je BTCS (Backward Time Centered Space). MKR je ustaljeni pristup koji za većinu pravilno definisanih prostornih domena radi veoma dobro. Za ovako jednostavnu postavku kao što je jednodimenziono provođenje toplote i kada su svi parametri problema poznati (ovde je to \(\alpha\)), MKR je često optimalna metoda. Međutim, kod većine problema iz prakse to nije slučaj. Hajde da razmotrimo kako da ovaj problem rešimo koristeći NMPFZ i direktno uporedimo sa MKR.

Rešavanje pomoću NMPFZ

Rešenje jednačine Sl. 3 sa već postavljenim graničnim i početnim uslovima:

(13)\[\begin{split}u(x=0,t)=u(x=1,t)=0, \, \forall t \\ u(x,t=0) = sin{(\pi x)}\end{split}\]

potražićemo pomoću NMPFZ pristupa. Iako je moguće da metode implementiramo direktno kao Raissi et al. [RPK19] koristeći okvir za duboko učenje kao što je Tensorflow, ipak ćemo iskoristiti pomoć biblioteka koje dodatno apstrahuju NMPFZ entitete i omogućavaju korisniku da se fokusira na problem koji rešava. Ovaj primer rešićemo koristeći biblioteku SCIANN autora Haghighat and Juanes [HJ21]. Postupak rešavanja objasnićemo direktno kroz programski kod:

Listing 1 NMPFZ - provođenje toplote
 1 import numpy as np
 2 import sciann as sn
 3 from sciann.utils.math import diff, sign, sin, sqrt, exp
 4 from numpy import pi
 5
 6 x = sn.Variable('x')
 7 t = sn.Variable('t')
 8 u = sn.Functional('u', [x,t], 3*[20], 'tanh')
 9 alpha = 0.3
10
11 L1 = diff(u, t) - alpha * diff(u, x, order=2)
12
13 TOLX = 0.011
14 TOLT = 0.0011
15 C1 = (1-sign(t - TOLT)) * (u - sin(pi*x))
16 C2 = (1-sign(x - (0+TOLX))) * (u)
17 C3 = (1+sign(x - (1-TOLX))) * (u)
18
19 m = sn.SciModel([x, t], [L1, C1, C2, C3], 'mse', 'Adam')
20
21 x_data, t_data = np.meshgrid(
22     np.linspace(0, 1, 101),
23     np.linspace(0, 0.1, 101)
24 )
25
26 h = m.train([x_data, t_data], 4*['zero'], learning_rate=0.002, batch_size=256, epochs=500)
27
28 # Test
29 nx, nt = 20, 10
30 x_test, t_test = np.meshgrid(
31     np.linspace(0.01, 0.99, nx+1),
32     np.linspace(0.01, 0.1, nt+1)
33 )
34 u_pred = u.eval(m, [x_test, t_test])

Varijable \(x\) i \(t\) se na početku definišu na propisani način. Osnovni pojam koji se koristi u SCIANN biblioteci za apstrakciju NMPFZ je funkcional, koji je ovde označen sa \(u\), koji kao ulaz uzima \(x\) i \(t\), ima 3 skrivena sloja sa po 20 neurona i kao aktivaciju svih tih neurona uzima funkciju hiperboličkog tangensa. Prvi sabirak kompozitne funkcije gubitka proizilazi iz same diferencijalne jednačine (10). Kao što se vidi, za diferenciranje se koristi specijalni operator diff() iz biblioteke:

L1 = diff(u, t) - alpha * diff(u, x, order=2)

Najzanimljiviji i ne baš tako očigledan je način definisanja početnog uslova C1 i graničnih uslova C2 i C3:

C1 = (1-sign(t - TOLT)) * (u - sin(pi*x))
C2 = (1-sign(x - (0+TOLX))) * (u)
C3 = (1+sign(x - (1-TOLX))) * (u)

Ovde je C1 jednak nuli u svim tačkama uzorkovanja osim za \(t \le TOLT\). Tolerancije TOLX i TOLT su postavljene tako da „hvataju” prvu/poslednju vrstu ili kolonu kolokacionih tačaka, u zavisnosti šta je potrebno. Umesto funkcije znaka sign(), mogu se koristiti i glatkije funkcije, kao što je hiperbolički tangens. NMPFZ model se formira pomoću SciModel konstruktora koji definiše i tip funkcije gubitka i algoritam optimizacije, tj. obučavanja:

m = sn.SciModel([x, t], [L1, C1, C2, C3], 'mse', 'Adam')

Obučavanje modela se pokreće metodom train(), pri čemu se navode sledeći parametri:

  1. Skup kolokacionih tačaka za treniranje. Ovde je to pravilna ekvidistantna mreža tačaka po obe varijable. Horizontala je prostor, a vertikala vreme.

  2. Početne vrednosti komponenti funkcije gubitka. Uobičajeno je da se na početku postave na nule.

  3. Stopa učenja,

  4. Veličina batch-a. Treba imati na umu da ako je broj tačaka domena u kojima se nameću granični uslovi značajno manji u odnosu na ukupan broj kolokacionih tačaka, parametar optimizacije batch_size treba da bude podešen na veliki broj koji garantuje doslednu optimizaciju mini batch-a. U suprotnom, može da se desi da neki mini batch-evi ne dobiju nijednu kolokacionu tačku koja pripada graničnim uslovima i stoga ne generišu tačan gradijent za ažuriranje metodom gradijentnog spusta.

  5. Broj epoha.

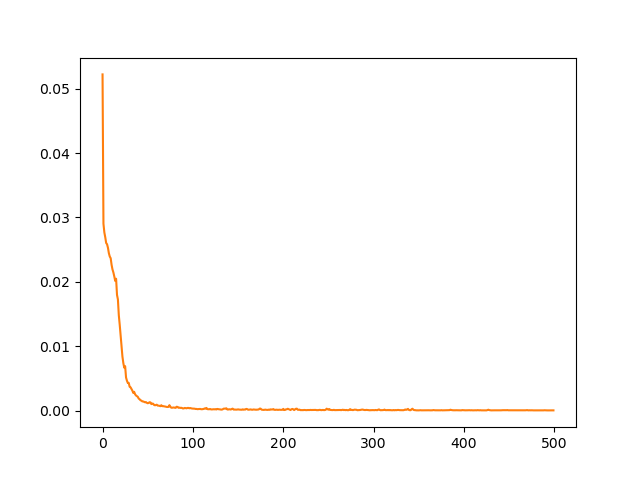
../_images/loss1.png

Sl. 7 Istorija obuke jednodimenzionog modela provođenja toplote.

Tok obuke možemo da ispratimo kroz standardne Tensorflow objekte, kao što je h.history['loss'], kao što se vidi na Sl. 7. Pošto se završi obuka NMPFZ-a, možemo formirati testni skup tačaka slično kao što smo to učinili i sa kolokacionim tačkama i proveriti rezultate predikcije pozivom metode eval() na objektu istreniranog modela. Rezultat polja temperature duž štapa u trenutku \(t=0,1\) i njegovo poređenje sa analitičkim rešenjem vidi se na Sl. 8.

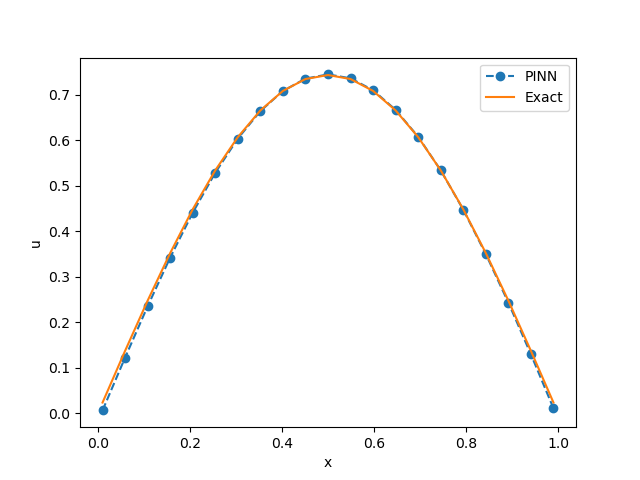
../_images/heat-pinn1.png

Sl. 8 Polje temperature duž štapa u trenutku \(t=0,1\) dobijeno metodom NMPFZ.

Čisto praktično gledano, NMPFZ rešenje jednostavnog direktnog problema kao što je ovaj i ne pruža nikakve posebne prednosti u odnosu na klasičnu MKR metodu. Prvo, rešavanje duže traje i zahteva upošljavanje više računarskih resursa i zavisnosti u vidu dodatnih biblioteka za tenzorski račun. Dalje, specifikacija početnih i graničnih uslova kod NMPFZ ima svoje specifičnosti. Treće, neophodno je metodom probe i greške podesiti hiper-parametre modela, kao što su: broj skrivenih slojeva, broj neurona po sloju, aktivaciona funkcija, brzina učenja (Learning Rate) itd. Od izbora hiper-parametara konvergencija rešenja može značajno da zavisi.

Sa druge strane, za razliku od MKR i MKE (Metoda Konačnih Elemenata), NMPFZ nam dozvoljava da problem definišemo čistim diferencijalnim jednačinama i proizvoljnim graničnim uslovima (Dirihleovi, Nojmanovi, periodični, skup tačaka). Nema potrebe za specificiranjem algebarske veze između čvorova (tj. kolokacionih tačaka u NMPFZ) i rešavanjem tako postavljenog sistema jednačina. Zahvaljujući ovoj činjenici, bilo koja nova fizika u vidu novog graničnog uslova ili promena u samoj diferencijalnoj jednačini može da se izvede veoma lako, omogućavajući brzu proveru hipoteza i izradu prototipova.

Drugo, dok sve klasične metode proračun moraju da izvedu kroz vremenske korake (time stepping), NMPFZ omogućava brzu inferenciju na već obučenoj mreži za bilo koji vremenski trenutak \(t\) postavljen na ulazu mreže. Za neke primene u realnom vremenu gde je brzina od ključnog značaja, ovo može da bude presudno.

Treće, NMPFZ metodološki ne razlikuje direktne probleme (u kojima se rešava poznata diferencijalna jednačina) od inverznih problema, kod kojih su neki od parametara nepoznati, ali postoje dodatni uslovi iz kojih se nepoznati parametri mogu dobiti procesom treninga. U narednoj temi Jednodimenzioni inverzni problem demonstriraćemo jedan takav problem.