Jednodimenzioni inverzni problem

Postavka inverznog problema je potpuno ista kao i u prethodnom poglavlju Jednodimenzioni direktni problem, tj. opisana je Sl. 3, jednačinom (10) i graničnim uslovima (13). Međutim, ovoga puta nam parametar problema \(\alpha\) na početku nije poznat i pokušaćemo da ga dobijemo uz pomoć metoda obučavanja propagacijom unazad. Naravno, čim smo uveli novu nepoznatu, moramo da uvedemo i novi granični uslov. Recimo, možemo da postavimo da je u jednoj tački u nekom vremenskom trenutku, temperatura \(u\) odgovarala nekoj numeričkoj vrednosti koja se poklapa sa analitičkim rešenjem (12). Recimo, postavimo temperaturu na sredini štapa u \(x=0,5\) u trenutku \(t=0,05\) na:

\[u(x=0,5, t=0,05) = 0,8623931,\]

i pokušajmo da rešimo problem postavljajući granične uslove na sledeći način:

Listing 2 Pronalaženje nepoznatog parametra \(\alpha\)
 1x = sn.Variable('x')
 2t = sn.Variable('t')
 3u = sn.Functional('u', [x,t], 3*[20], 'tanh')
 4alpha = sn.Parameter(0.5, inputs=[x,t], name="alpha")
 5
 6L1 = diff(u, t) - alpha * diff(u, x, order=2)
 7
 8TOL = 0.011
 9TOLT= 0.0011
10C1 = (1-sign(t - TOLT)) * (u - sin(pi*x))
11C2 = (1-sign(x - (0+TOL))) * (u)
12C3 = (1+sign(x - (1-TOL))) * (u)
13C4 = (1 + sign(t-0.049)) * (1 - sign(t-0.051)) * (1 + sign(x-0.49)) * (1 - sign(x-0.51)) * (u-0.8623931)
14
15m = sn.SciModel([x, t], [L1, C1, C2, C3, C4], 'mse', 'Adam')
16
17x_data, t_data = np.meshgrid(
18    np.linspace(0, 1, 101),
19    np.linspace(0, 0.1, 101)
20)
21
22h = m.train([x_data, t_data], 5*['zero'], learning_rate=0.002, batch_size=512, epochs=1200,
23    adaptive_weights={'method':'NTK', 'freq':100})
24
25# Test
26nx, nt = 20, 10
27x_test, t_test = np.meshgrid(
28    np.linspace(0.01, 0.99, nx+1),
29    np.linspace(0.01, 0.1, nt+1)
30)
31u_pred = u.eval(m, [x_test, t_test])
32
33print(alpha.value)

Očigledno je da je kod gotovo isti kao prethodni u kome se rešava direktni problem, jer je i metodologija za rešavanje direktnih i inverznih problema kod NMPFZ identična. Jedina razlika je u postavci. Linija 4 postavlja \(\alpha\) kao nepoznati parametar i daje mu početnu vrednost. U liniji 13 se postavlja dodatni granični uslov u tački u(x=0.4,t=0.05), koji će postati još jedna komponenta kompozitne funkcije gubitka koja se formira u liniji 15. Vrednost nepoznatog parametra se štampa u poslednjoj liniji i u našem testu iznosi oko 0,308, što je dovoljno blisko realnoj vrednosti od 0,3. Potvrda zadovoljavajućeg rešenja inverznog problema prikazana je i grafički na Sl. 9.

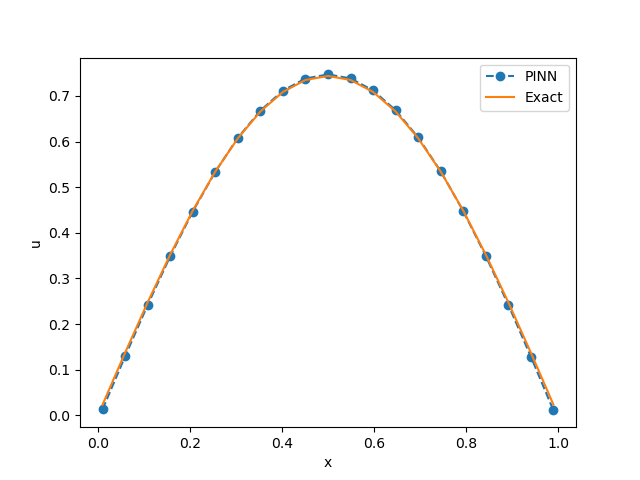
../_images/heat-inv.png

Sl. 9 Polje temperature duž štapa u trenutku \(t=0,1\) dobijeno rešavanjem inverznog problema