Stefanov problem u modelima topljenja

Nakon što smo uspešno rešili i direktni i inverzni problem provođenja toplote koji je opisan jednostavnom paraboličnom parcijalnom diferencijalnom jednačinom, pozabavićemo se malo komplikovanijom postavkom sličnog problema, pre svega imajući u vidu granične uslove. Ovde će se oni dinamički menjati u zavisnosti od gradijenta temperature. Pokazaćemo da je zapravo ovako postavljen problem lakše i prirodnije rešavati pomoću NMPFZ-a nego pomoću klasičnih numeričkih metoda baziranih na mreži integracionih tačaka (MKE, MKR).

Stefanovi problemi faznih promena imaju primenu u raznim oblastima nauke i inženjerstva, kada god se faza posmatrane supstance menja između tečnog, čvrstog ili gasovitog stanja. Pretpostavlja se da materijal prolazi kroz faznu promenu sa kretanjem granice, čiji je položaj nepoznat i mora se odrediti kao deo same numeričke analize. Pošto problemi sa pomeranjem granica zahtevaju rešavanje toplotne jednačine u nepoznatoj oblasti koja se takođe mora odrediti kao deo rešenja, oni su inherentno nelinearni.

Problem jednodimenzionalne promene faze mogao bi se demonstrirati pomoću polubeskonačnog čvrstog tela, kao što je tanak blok leda koji zauzima \(0 \le x < \infty\), na temperaturi očvršćavanja. Na fiksnoj granici tankog bloka leda \(x=0\), mogu da deluju različite vrste fluksa. U ovom primeru koristimo isti granični uslov kao Ivanovic et al. [ISS17], Savovic and Caldwell [SC09], tako se temperatura pri \(x=0\) povećava eksponencijalno sa vremenom. Takođe, propisujemo da se čitava čvrsta faza nalazi na temperaturi topljenja. Stoga svodimo problem na određivanje raspodela temperature u tečnoj fazi u vreme \(t_0\), gde je \(x < s(t_0)\), kao i položaja granice između faza \(s(t_0)\).

U nekom kasnijem vremenskom trenutku \(t_1 > t_0\), pokretna granica \(s(t)\) kreće se udesno, zauzimajući poziciju \(s(t_1) > s (t_0) = s_0\), kao što je prikazano na Sl. 10. Deo tankog bloka leda od pozicije \(s(t_0)\) do pozicije \(s(t_1)\), otopio se tokom vremenskog intervala \((t_0,t_1)\).

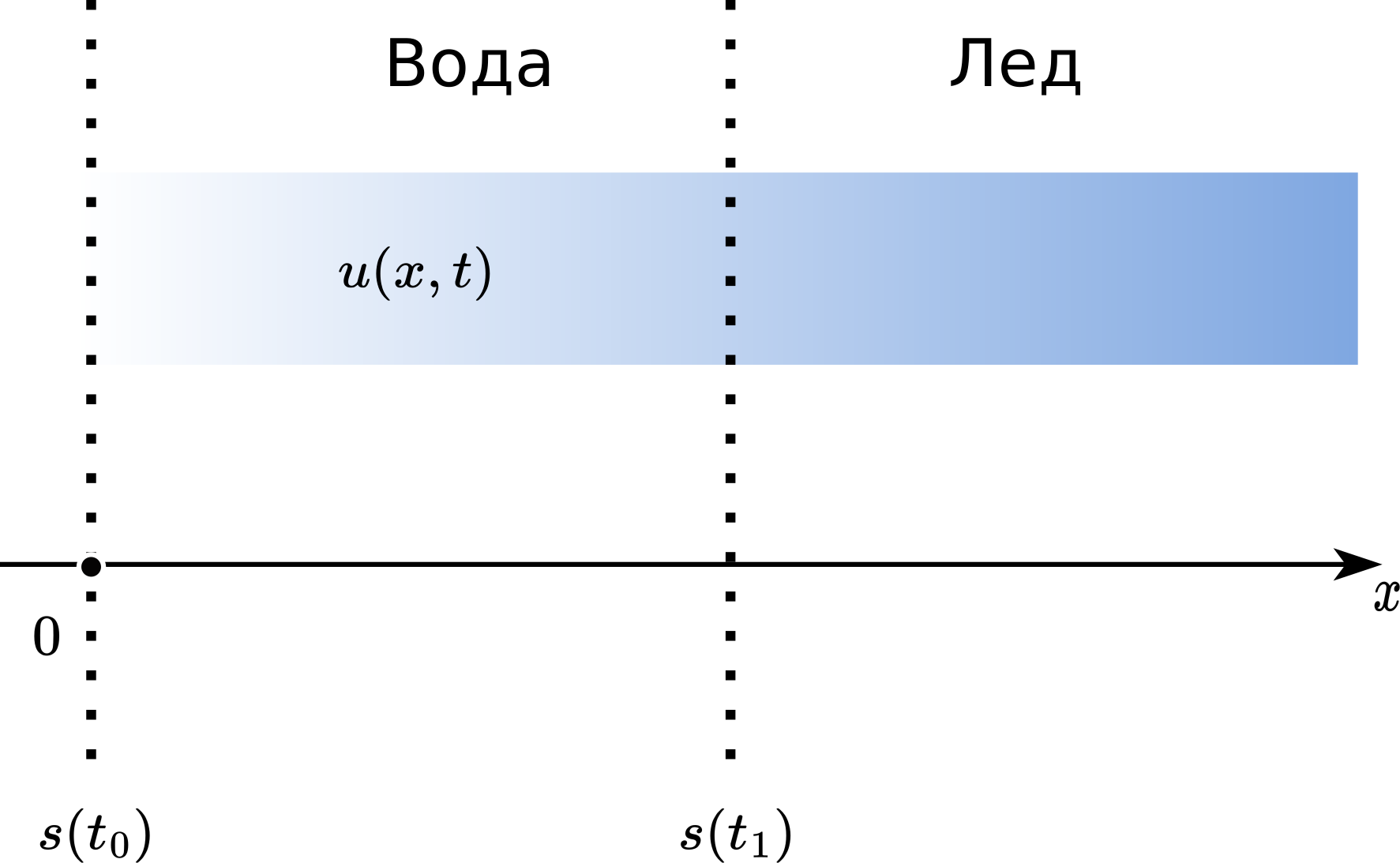
../_images/stefann.png

Sl. 10 Stefanov problem u jednoj dimenziji. \(s(t)\) označava pokretnu granicu, a \(u(x,t)\) temperaturu tečne faze (za \(x<s\)).

Distribucija temperature \(u(x,t)\) u regionu u kome vlada tečno stanje \(0 \le x \le s(t)\) data je toplotnom jednačinom:

\[\frac{\partial u}{\partial t} = \alpha \cdot \frac{\partial^2 u}{\partial x^2},\]

koja može da se napiše na sledeći način:

(14)\[\frac{\partial u}{\partial t} - \alpha \cdot \frac{\partial^2 u}{\partial x^2} = 0,\]

pod sledećim graničnim uslovima:

(15)\[\begin{split}u(x,t) = e^{\alpha t}, \quad x = 0, \quad t > 0 \\ u(x,t) = 1,\quad x = s(t), \quad t > 0.\end{split}\]

Ovde \(\alpha\), kao i u prethodnim primerima označava fizički parametar koji kombinuje toplotnu provodnost, gustinu i specifičnu toplotu. Pozicija pokretne granice data je jednačinom koja je poznata kao Stefanov uslov:

(16)\[\frac{1}{\alpha} \cdot \frac{ds}{dt} = - \frac{\partial u}{\partial x}, \quad x = s(t), \quad t > 0.\]

U opštem slučaju, početni uslov za položaj granice faza dat je sa:

(17)\[s(0) = 0.\]

Za ovako postavljen problem poznato je i analitičko rešenje, i to:

\[\begin{split}u(x,t) = e^{\alpha t - x} \\ s(t) = \alpha t.\end{split}\]

Rešavanje ovog problema NMPFZ pristupom podrazumeva konstrukciju dve neuronske mreže. Prva će aproksimirati distribuciju temperatura \(u(x,t)\) dok će druga aproksimirati položaj slobodne granice između faza \(s(t)\). Aproksimativna rešenja biće automatski diferencirana u odnosu na ulazne varijable od kojih zavise, za vrednosti definisane skupom kolokacionih tačaka iz domena \(\lbrack 0,T\rbrack \times \mathcal{D}\), gde je \(\mathcal{D \subset}\mathbb{R}^{d}\) ograničeni domen, a \(T\) označava konačno vreme simulacije. Funkcija gubitka sastoji se iz komponenti izvedenih iz (14), (15) i (17), koristeći aproksimacije za \(u\) i \(s\) u kolokacionim tačkama, koje pokrivaju kako unutrašnjost domena, tako i domene u kojima važe početni i granični uslovi.

Konstrukcija funkcije gubitka

Kao što je već rečeno, prva mreža aproksimira funkciju temperature \(u(x,t)\), a druga mreža aproksimira položaj slobodne granice između faza \(s(t)\). Funkcija gubitka sastoji se iz razlike \(u\) i \(s\) i njihovih aproksimacija \(\widehat{u}\) i \(\widehat{s}\) koje daje NMPFZ i koji predstavljaju reziduume koje daje glavna diferencijalna jednačina, početni i granični uslovi. Dakle, ukupan gubitak \(\mathcal{L}\) određen je sumom reziduuma:

(18)\[\mathcal{L} = \mathcal{L}_r + \mathcal{L}_0 + \mathcal{L}_{b_{1}} + \mathcal{L}_{b_{2}} + \mathcal{L}_{b_{3}},\]

gde su:

(19)\[\begin{split}\mathcal{L}_r = \frac{1}{N_r}\sum_{i = 1}^{N_r}{\left| \frac{\partial\widehat{u}(x,t)}{\partial t} - \alpha\frac{\partial^{2}\widehat{u}(x,t)}{\partial x^2} \right|^2}, \\ \mathcal{L}_0 = \frac{1}{N_{0}}\sum_{i = 1}^{N_0}{\left| \widehat{s}(0) - s(0) \right|^2}, \\ \mathcal{L}_{b_1} = \frac{1}{N_{b_1}}\sum_{i = 1}^{N_{b_1}}\left| \frac{1}{a}\frac{\partial\widehat{s}(t)}{\partial t} + \frac{\partial\widehat{u}}{\partial\widehat{s}(t)} \right|^2, \\ \mathcal{L}_{b_2} = \frac{1}{N_{b_2}}\sum_{i = 1}^{N_{b_2}}\left| \widehat{u}(0,t) - u(0,t) \right|^{2}, \\ \mathcal{L}_{b_3} = \frac{1}{N_{b_3}}\sum_{i = 1}^{N_{b_3}}\left| \widehat{u}\left( \widehat{s}(t),t \right) - u\left( s(t),t \right) \right|^2.\end{split}\]

Prvi član \(\mathcal{L}_r\) penalizuje po glavnoj diferencijalnoj jednačini (14), gde je \(N_r\) veličina batch-a kolokacionih tačaka koje se slučajno uzorkuju iz domena prostor-vremenskih koordinata koje uzimaju vrednosti \(0 \leq x \leq 1\) i \(0s \leq t \leq 0,5s\), respektivno. \(\widehat{u}(x,t)\) je aproksimativna neuronska mreža temperaturskog polja \(u(x,t)\). Drugi član \(\mathcal{L}_0\) određuje ispunjenost graničnog uslova (17). Ispunjenost Stefanovog graničnog uslova (16) dat je reziduumom \(\mathcal{L}_{b_1}\), gde \(\widehat{s}(t)\) označava NMPFZ aproksimaciju položaja pokretne granice. Poslednja dva člana \(\mathcal{L}_{b_2}\) i \(\mathcal{L}_{b_3}\) određuju reziduale graničnih uslova (15), gde \(N_0, \, N_{b_1}, \, N_{b_2}\), i \(N_{b_3}\) označavaju broj kolokacionih tačaka u kojima važe početni i granični uslovi.

Implementacija

Rešenje koje koristi funkcionalnost već poznate biblioteke SCIANN dato je u sledećem listingu:

Listing 3 Rešenje Stefanovog problema u 1D korišćenjem SCIANN biblioteke
 1alpha = 1.0
 2
 3# Pocetni uslovi
 4t0 = 0.1
 5s0 = alpha * t0
 6
 7# Varijable
 8x = sn.Variable('x')
 9t = sn.Variable('t')
10u = sn.Functional (["u"], [x, t], 3*[30] , 'tanh')
11s = sn.Functional (["s"], [t], 3*[30] , 'tanh')
12
13# Glavna dif. jednacina
14L1 =  diff(u, t) - alpha * diff(u, x, order=2)
15
16TOLX=0.004
17TOLT=0.002
18
19# Stefanov uslov
20C1 = (1/alpha*diff(s, t) + diff(u,x)) * (1 + sign(x - (s-TOLX))) * (1-sign(x-s))
21# Pocetno s u trenutku t=t0
22C2 = ( s - s0 ) * (1-sign(t - (t0+TOLT)))
23# Granicni uslov za u kada je x=0
24C3 = ( u - exp(alpha*t) ) * (1-sign(x - (0 +TOLX)))
25# Temperatura na granici izmedju faza je 1
26C4 = (u-1) * (1-sign(x - (s+TOLX))) * (1+sign(x-s))
27
28x_data, t_data = [], []
29
30# Trening skup
31x_train, t_train = np.meshgrid(
32    np.linspace(0, 1, 300),
33    np.linspace(t0, 0.5, 300)
34)
35
36x_data, t_data = np.array(x_train), np.array(t_train)
37
38m = sn.SciModel([x, t], [L1,C1,C2,C3,C4], 'mse', 'Adam')
39h = m.train([x_data, t_data], 5*['zero'], learning_rate=0.002, batch_size=1024, epochs=200, adaptive_weights={'method':'NTK', 'freq':20})
40
41# Test
42x_test, t_test = np.meshgrid(
43    np.linspace(0, 1, 30),
44    np.linspace(0.01, 0.5, 30)
45)
46u_pred = u.eval(m, [x_test, t_test])
47s_pred = s.eval(m, [x_test, t_test])
48
49s=[]
50for e in s_pred:
51    s.append(e[0])

Na početku (linije 1-11) postavljamo konstante i varijable. Primetimo da modelovanje kreće od vremenskog trenutka \(t_0=0,1s\). Prva zagrada u izrazu za C1

C1 = (1/alpha*diff(s, t) + diff(u,x)) * (1 + sign(x - (s-TOLX))) * (1-sign(x-s))

predstavlja sam Stefanov uslov. Kao što je uobičajeno za postavljanje graničnih uslova, druga zagrada postavlja pravilo gde taj granični uslov važi. Za C1 je taj izraz malo komplikovaniji zbog tolerancije, ali zapravo predstavlja uslov da je \(x \approx s\). Uslov

C2 = ( s - s0 ) * (1-sign(t - (t0+TOLT)))

definiše položaj granice u početnom trenutku. Dalje, uslov

C3 = ( u - exp(alpha*t) ) * (1-sign(x - (0 +TOLX)))

postavlja dinamički uslov promene temperature u tački \(x=0\) prema jednačini (15). Konačno, posledlji uslov

C4 = (u-1) * (1-sign(x - (s+TOLX))) * (1+sign(x-s))

u istom skupu kolokacionih tačaka kao što je to bio slučaj sa uslovom C1, tj. na granici između faza \(x \approx s\) postavlja vrednost temperature na 1. Ostatak koda je manje-više standardno treniranje, formiranje testnog skupa i ekstrakcija podataka o kretanju granice s kroz vreme. Kretanje granice između faza kroz vreme može se videti na Sl. 11, dok se polje temperature \(u(x,t=0,5)\) može videti na Sl. 12.

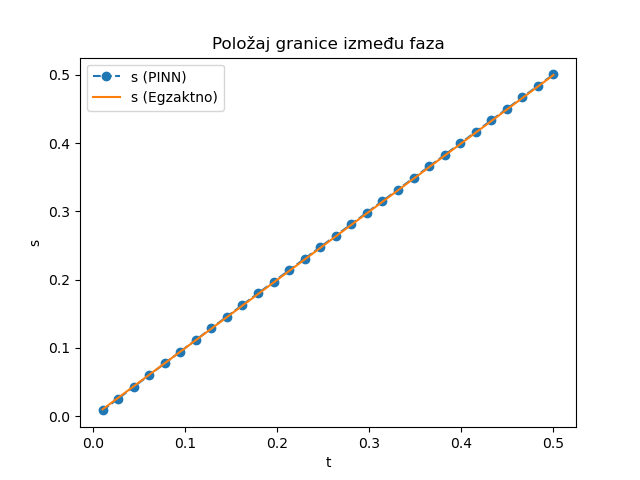
../_images/stefan-s.png

Sl. 11 Kretanje granice između faza \(s(t)\) tokom vremena.

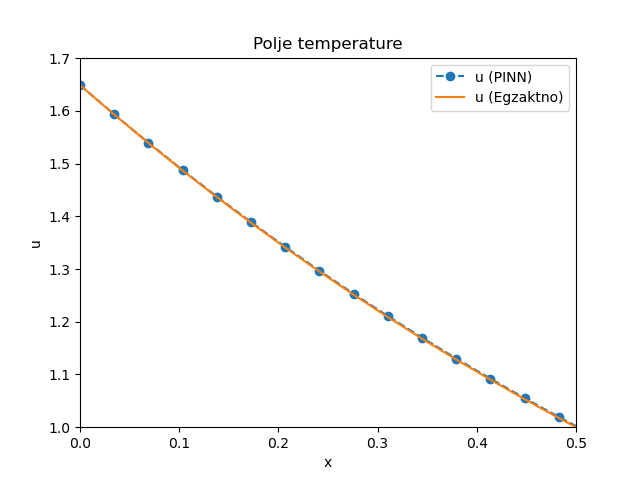
../_images/stefan-u.png

Sl. 12 Polje temperatura \(u(x,t)\) u trenutku \(t=0,5\)

Sa dijagrama je očigledno da se NMPFZ (PINN) rešenja u zadovoljavajućoj meri slažu sa analitičkim rešenjem za posmatranu pojavu. U skladu sa prethodnom opštom diskusijom o upotrebnoj vrednosti NMPFZ pristupa, kod direktnih problema kao što je ovaj, dodatna vrednost u odnosu na klasične numeričke metode može se naći u jednostavnijoj formulaciji. Međutim, tek kod inverznih problema, kada su i neki od parametara nedovoljno poznati, pristup učenja propagacijom unazad pokazuje svoju pravu snagu. Sledeći odeljak uvodi nepoznati parametar u ovaj isti problem.

Inverzni 1-D Stefanov problem

Pretpostavim identičnu postavku Stefanovog problema, osim što sada nije poznata vrednost materijalnog parametra \(\alpha\), pa time ni potpuni oblik diferencijalne jednačine, ali je zato poznato da je, na primer, u trenutku \(t=0,2\) granica između faza uočena na koordinati \(x=0,2\). Nepoznati parametar uvešćemo formulacijom:

# Nepoznati parametar
alpha = sn.Parameter(2.5, inputs=[x,t])

Parametru je data početna vrednost od 2,5 i postavljena zavisnost od obe ulazne varijable \(x\) i \(t\). Dodatni granični uslov C5 dat je standardno:

# Dodatni uslov u tacki s(t=0.2)=0.2
C5 = (1-sign(t - (0.2+TOLT))) * (1+sign(t-0.2)) * (s-0.2)

Iako je ovog puta potrebno nešto više epoha u procesu treninga, jer je početna vrednost nepoznatog parametra \(\alpha\) (2,5) prilično daleko od realne vrednosti (1), algoritam koji koristi brzinu učenja od 0,001 u stotinak epoha dolazi do vrednosti \(\alpha=0,99\) i zaista zadovoljavajućeg poklapanja sa analitičkim rešenjem, kao što se vidi na Sl. 13 za kretanje granice i za polje temperature u \(u(x,t=0,5)\) na Sl. 14.

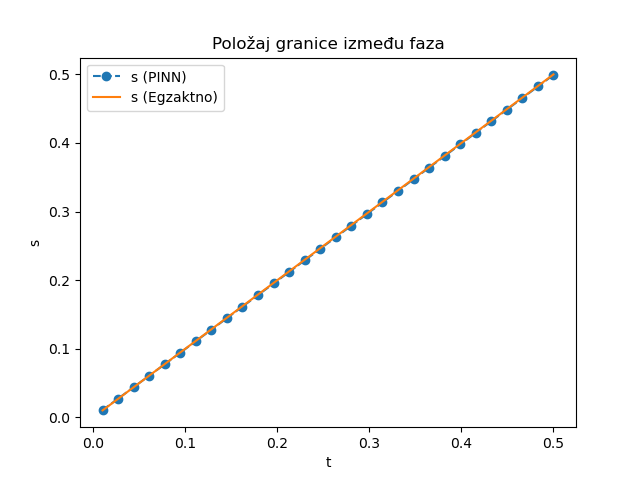
../_images/stefan-inv-s.png

Sl. 13 Kretanje granice između faza \(s(t)\) tokom vremena za inverzni problem

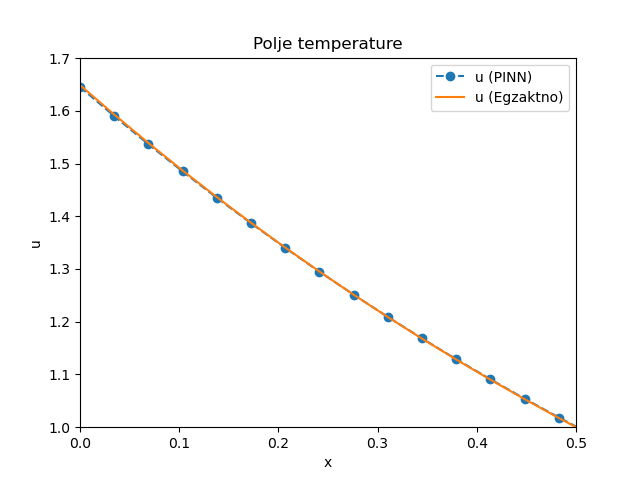
../_images/stefan-inv-u.png

Sl. 14 Polje temperatura \(u(x,t)\) u trenutku \(t=0,5\) za inverzni problem