Увод

Хаксли и Хоџкин су 1957. године развили биофизички модел који је био основа за сва наредна истраживања у овој области Huxley [Hux57]. Природа Хакслијевог модела се ослања на динамику попречних мостова, због чега је сама теорија и названа теорија попречних мостова Huxley [Hux57]. Детаље везане за анатомију и физиологију мишића не можемо излагати у овом типу литературе, већ се читалац упућује на Svičević [Svivcevic20].

Хаксли је разматрао половину саркомере и сматрао је да су главе миозина за миозински филамент причвршћене помоћу еластичних веза. На Сл. 45 имамо шематску репрезентацију модела, на којој се може уочити да је дебели миозински филамент фиксиран у простору за М-линију. Приликом стимулације мишића очекивано је да се миозинске главе вежу на најближе слободно место на актину, услед чега долази до формирања еластичних веза у виду попречних мостова. У том тренутку долази до генерисања активне мишићне силе.

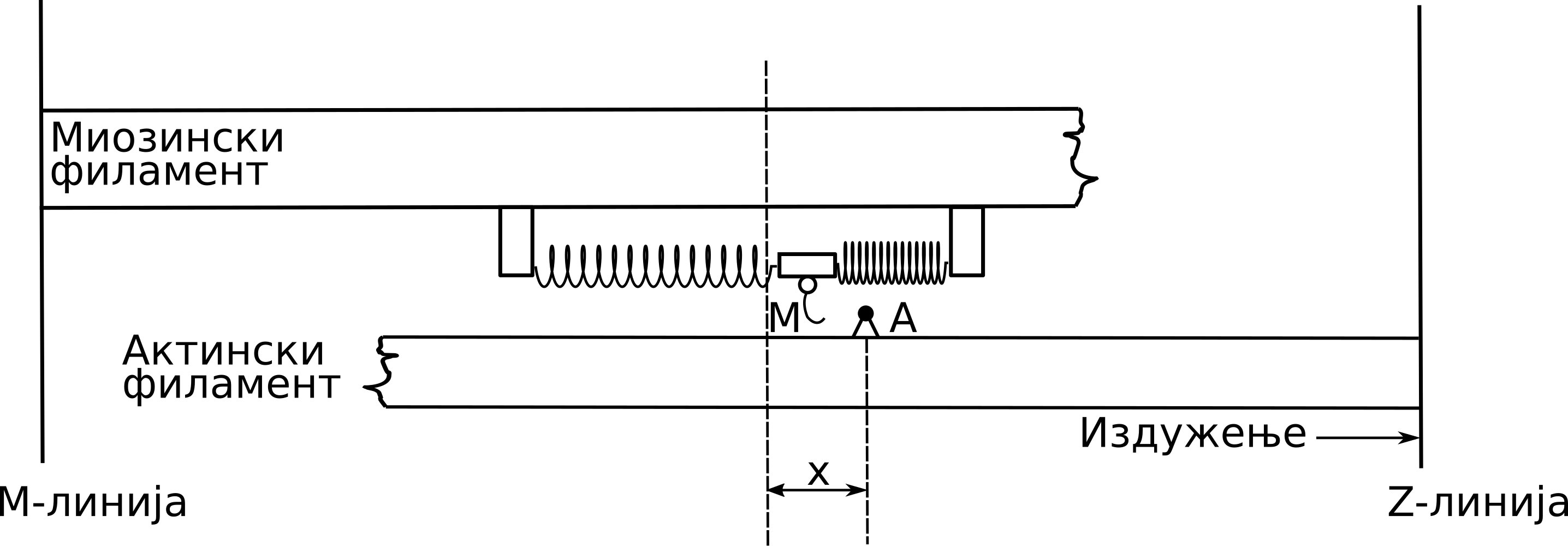
Сл. 45 Хакслијев модела клизајућих филамената

Сила се тада преноси на актински филамент који се том приликом креће ка Z-линији. Процес формирања попречних мостова се понавља услед сталног релативног клизања актинског филамента дуж миозинског и зависи од положаја самих миозинских глава. Том приликом, попречни мостови трпе истезања и скраћивања. Због сталног релативног клизања филамената, Хакслијева теорија се назива и Теоријом клизајућих филамената Huxley [Hux57].

У случају издужења мишића, актински филамент клизи удесно, дуж миозинског филамента, који је фиксиран за М-линију. Померање главе миозина од њене усправне позиције, у правцу М-линије или Z-линије до активног места А на актинском филаменту, означено је са \(x\) и тумачи се као дужина попречног моста. У једном тренутку, миозинска глава може бити везана само за једно активно место актина, при чему je померање ограничено максималним померањем главе миозина, изазваним термичким флуктуацијама, \(h\) , тако да важи \(0<x<h\).Уколико дужина попречног моста постане већа од \(h\) , долази до раскидања ове везе између филамената. У сваком тренутку је могуће идентификовати да ли је нека миозинска глава закачена или не, и да ли том приликом формира попречни мост дужине \(x\). Вероватноћа да случајно изабрана миозинска глава у тренутку \(t\) формира попречни мост дужине \(x\) из домена \(\Omega\) , означена је са \(n(x,t)\).

Вероватноћа \(n(x,t)\) се може тумачити и као удео броја миозинских глава које су у тренутку \(t\) закачене на растојању \(x\) у односу на укупан број миозинских глава. Овај број зависи од брзине успостављања и раскидања попречних мостова, тако да се континуиран процес стварања и раскидања попречних мостова може формулисати једначином:

(33)\[\frac{dn(x,t)}{dt} = \left[ 1-n(x,t) \right] f(x) - n(x,t) g(x),\]

где су \(f(x)\) и \(g(x)\) редом стопе успостављања и раскидања везе између миозина и актина у јединици времена, које зависе од растојања \(x\), као на Сл. 46. Вероватноћа успостављања везе је представљена производом удела оних миозинских глава које још увек нису закачене, \(1-n(x,t)\), и стопе успостављања везе, \(f(x)\). С друге стране, вероватноћа да се успостављена веза између актина и миозина прекине је дата као \(n(x,t) g(x)\).

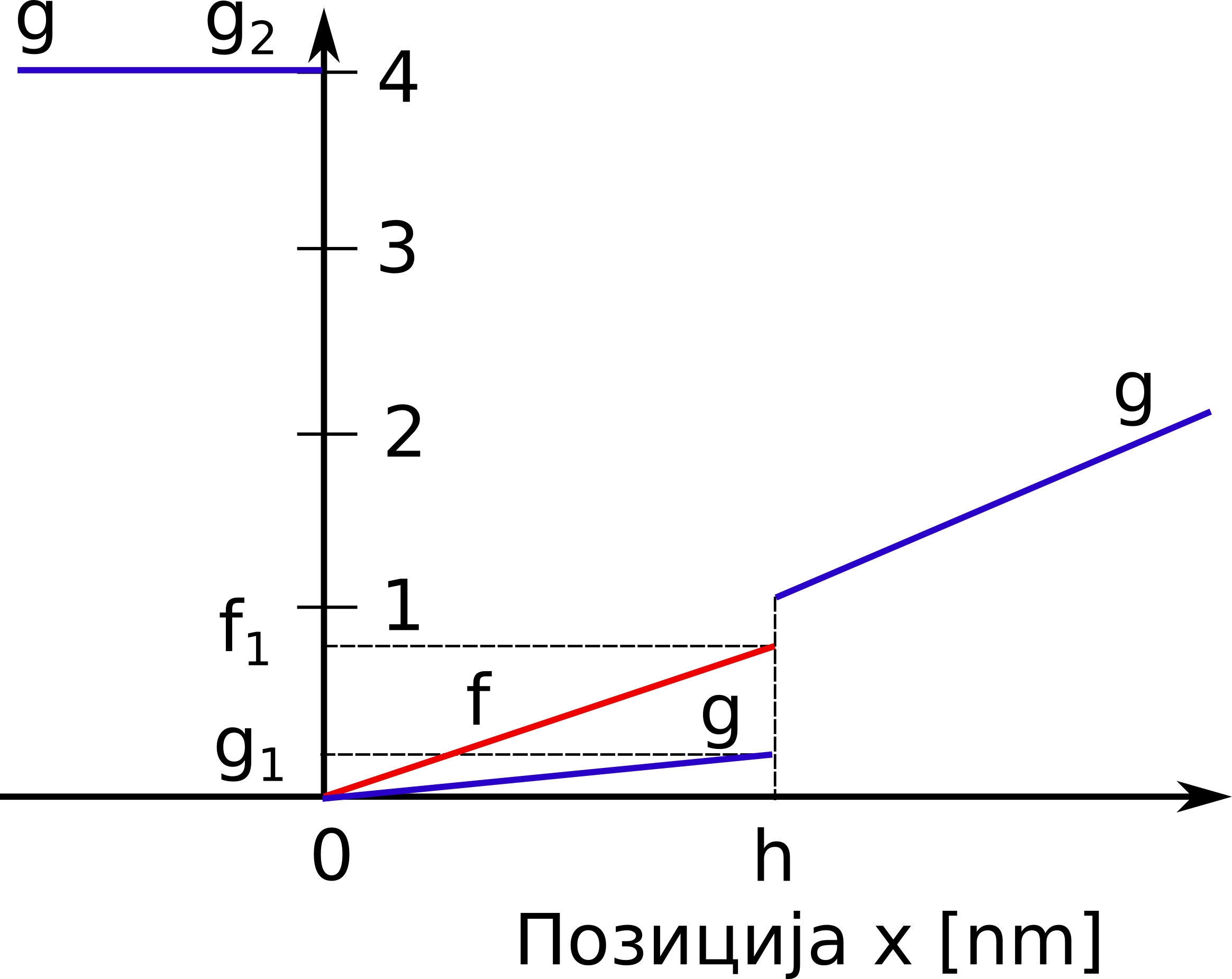
Сл. 46 Стопе успостављања везе, \(f\), (наранџаста линија) и раскидања везе, \(g\), (плава линија) између миозина и актина

Хакслијева теорија кинетике попречних мостова се може изразити коришћењем парцијалне диференцијалне једначине над доменом \(\Omega\):

\[\frac{\partial n}{\partial t} (x,t) - v \frac{\partial n}{\partial x} = \mathcal{N} \left( n(x,t), x\right), \qquad \forall x \in \Omega,\]

где је \(v= -dx/dt\) брзина клизања филамента актина у односу на филамент миозина (позитивна при контракцији), а

\[\mathcal{N} \left( n(x,t), x\right) = \left[ 1-n(x,t) \right] f(x) - n(x,t) g(x)\]

представља брзину промене стања попречних мостова.

У циљу што реалистичнијег описа понашања мишића током издужења, Захалак је увео одређене модификације оригиналног Хакслијевог модела. Увео је минималне промене у дефиницији стопа успостављања и раскидања веза између миозина и актина, тако да је при скраћивању мишића све остало непромењено, док је при издужењу омогућио већу стопу откачињања. Ово је практично реализовано тако што је уведен Захалаков фактор, \(f_{Zah}\), у случају када је дужина попречног моста \(x\) већа од \(h\):

(34)\[\begin{split}x<0 \quad : \quad f(x)=0; \, g(x)=g_2; \\ 0 \le x \le h \quad : \quad f(x)=f_1 x/h; \, g(x)=g_1 x/h; \\ x>h \quad : \quad f(x)=0; \, g(x)=f_{Zah} \, g_1 x / h\end{split}\]

Може се уочити да је у области \(x<0\) дефинисана висока вредност стопе откачињања, \(g(x)=g_2\) , како би се попречни мостови који су доспели у ову зону брзо прекинули. Постоји извесна стопа откачињања и у области \(0<x<h\), али је ниска у поређењу са негативном облашћу.

Након завршене обуке неуронске мреже, она се може користити као замена за метод карактеристика објашњен у Svičević [Svivcevic20]. Овде ћемо се зауставити са објашњавањем математичког модела, а читаоца који се интересује за изучавање ове области упутити на Svičević [Svivcevic20].