Решења директног проблема

Сада ћемо се позабавити резултатима процеса учења који смо успоставили у претходној секцији Имплементација.

Подпригушени случај

За случај да је:

\[\begin{split}m = 1 \\ \mu = 0,1 \\ k = 2\end{split}\]

имамо да су:

\[\begin{split}\delta = \frac{\mu}{2m} = 0,05 \\ \omega_0 = \sqrt{\frac{k}{m}} = \sqrt{2}\end{split}\]

Како је \(\delta^2-\omega_0^2 < 0\), имаћемо два конјуговано-комплексна решења, тј. подпригушени случај описан у секцији Подпригушени случај. Решења добијена скриптом датом у Имплементација, где су почетни услови постављени тако да је \((x_0=0, v_0=2)\) приказана су на Сл. 19.

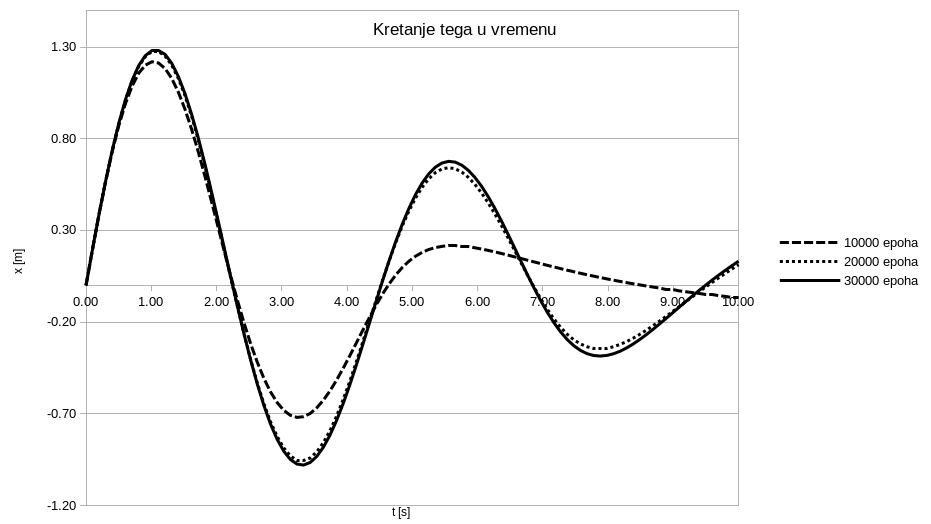
Сл. 19 НМПФЗ решење промене положаја тега у току времена за подпригушени случај осциловања.

На графику се може видети како се резултати разликују у односу на то колико епоха је мрежа тренирана. Наиме, резултати за 10000 епоха су значајно лошији него они за 20000 и 30000 епоха. Дакле, као и код готово свих проблема дубоког учења и код НМПФЗ тај процес треба пратити (Сл. 20) и тренинг прекинути тек када је досегнут одговарајући минимум и учење даље не напредује значајно.

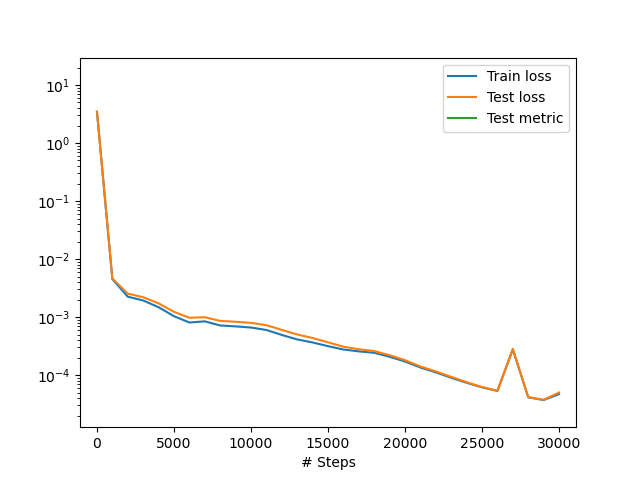
Сл. 20 Функција губитка у току процеса учења.

Препригушени случај

Уколико је, на пример:

\[\begin{split}m = 1 \\ \mu = 3 \\ k = 1\end{split}\]

имамо да су:

\[\begin{split}\delta = \frac{\mu}{2m} = 1,5 \\ \omega_0 = \sqrt{\frac{k}{m}} = 1\end{split}\]

Како је \(\delta^2-\omega_0^2 > 0\), имаћемо два различита реална решења, тј. препригушени случај описан у секцији Препригушени случај. Решења добијена скриптом датом у Имплементација за почетне услове \((x_0=0, v_0=2)\) приказана су на Сл. 21.

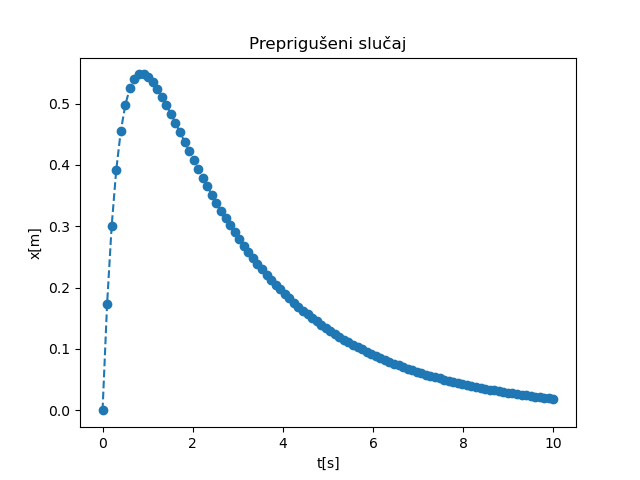
Сл. 21 НМПФЗ решење промене положаја тега у току времена за препригушени случај осциловања.

Критично-пригушени случај

Преостао је још критично-пригушени случај, који ће се добити уколико поставимо следеће параметре проблема:

\[\begin{split}m = 1 \\ \mu = 3 \\ k = 2,25\end{split}\]

Имамо да су:

\[\begin{split}\delta = \frac{\mu}{2m} = 1,5 \\ \omega_0 = \sqrt{\frac{k}{m}} = 1,5\end{split}\]

Како је \(\delta^2-\omega_0^2 = 0\), имаћемо два једнака реална решења, тј. критично-пригушени случај описан у секцији Критично-пригушени случај. Решења добијена скриптом датом у Имплементација за почетне услове \((x_0=0, v_0=2)\) приказана су на Сл. 22.

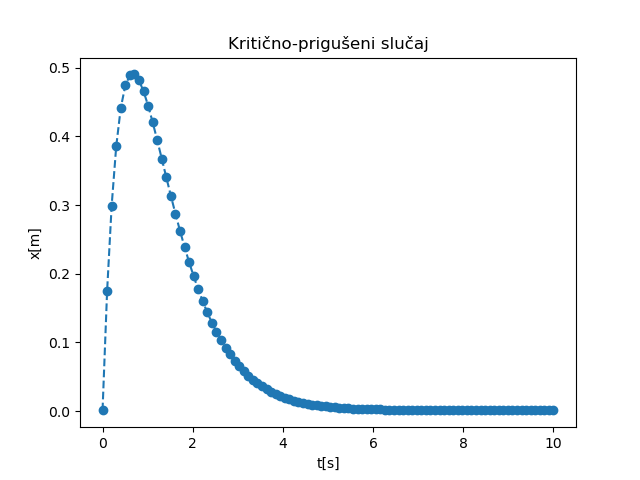
Сл. 22 НМПФЗ решење промене положаја тега у току времена за критично-пригушени случај осциловања.