Uvod

Haksli i Hodžkin su 1957. godine razvili biofizički model koji je bio osnova za sva naredna istraživanja u ovoj oblasti Huxley [Hux57]. Priroda Hakslijevog modela se oslanja na dinamiku poprečnih mostova, zbog čega je sama teorija i nazvana teorija poprečnih mostova Huxley [Hux57]. Detalje vezane za anatomiju i fiziologiju mišića ne možemo izlagati u ovom tipu literature, već se čitalac upućuje na Svičević [Svivcevic20].

Haksli je razmatrao polovinu sarkomere i smatrao je da su glave miozina za miozinski filament pričvršćene pomoću elastičnih veza. Na Sl. 45 imamo šematsku reprezentaciju modela, na kojoj se može uočiti da je debeli miozinski filament fiksiran u prostoru za M-liniju. Prilikom stimulacije mišića očekivano je da se miozinske glave vežu na najbliže slobodno mesto na aktinu, usled čega dolazi do formiranja elastičnih veza u vidu poprečnih mostova. U tom trenutku dolazi do generisanja aktivne mišićne sile.

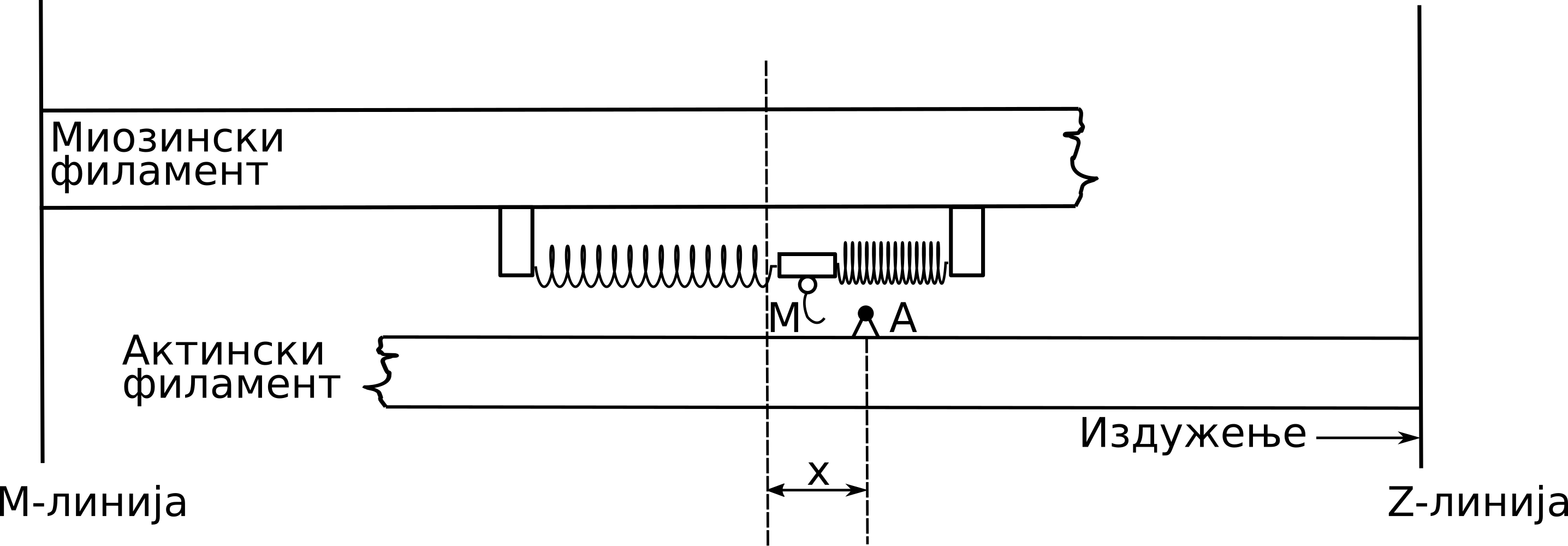
Sl. 45 Hakslijev modela klizajućih filamenata

Sila se tada prenosi na aktinski filament koji se tom prilikom kreće ka Z-liniji. Proces formiranja poprečnih mostova se ponavlja usled stalnog relativnog klizanja aktinskog filamenta duž miozinskog i zavisi od položaja samih miozinskih glava. Tom prilikom, poprečni mostovi trpe istezanja i skraćivanja. Zbog stalnog relativnog klizanja filamenata, Hakslijeva teorija se naziva i Teorijom klizajućih filamenata Huxley [Hux57].

U slučaju izduženja mišića, aktinski filament klizi udesno, duž miozinskog filamenta, koji je fiksiran za M-liniju. Pomeranje glave miozina od njene uspravne pozicije, u pravcu M-linije ili Z-linije do aktivnog mesta A na aktinskom filamentu, označeno je sa \(x\) i tumači se kao dužina poprečnog mosta. U jednom trenutku, miozinska glava može biti vezana samo za jedno aktivno mesto aktina, pri čemu je pomeranje ograničeno maksimalnim pomeranjem glave miozina, izazvanim termičkim fluktuacijama, \(h\) , tako da važi \(0<x<h\).Ukoliko dužina poprečnog mosta postane veća od \(h\) , dolazi do raskidanja ove veze između filamenata. U svakom trenutku je moguće identifikovati da li je neka miozinska glava zakačena ili ne, i da li tom prilikom formira poprečni most dužine \(x\). Verovatnoća da slučajno izabrana miozinska glava u trenutku \(t\) formira poprečni most dužine \(x\) iz domena \(\Omega\) , označena je sa \(n(x,t)\).

Verovatnoća \(n(x,t)\) se može tumačiti i kao udeo broja miozinskih glava koje su u trenutku \(t\) zakačene na rastojanju \(x\) u odnosu na ukupan broj miozinskih glava. Ovaj broj zavisi od brzine uspostavljanja i raskidanja poprečnih mostova, tako da se kontinuiran proces stvaranja i raskidanja poprečnih mostova može formulisati jednačinom:

(33)\[\frac{dn(x,t)}{dt} = \left[ 1-n(x,t) \right] f(x) - n(x,t) g(x),\]

gde su \(f(x)\) i \(g(x)\) redom stope uspostavljanja i raskidanja veze između miozina i aktina u jedinici vremena, koje zavise od rastojanja \(x\), kao na Sl. 46. Verovatnoća uspostavljanja veze je predstavljena proizvodom udela onih miozinskih glava koje još uvek nisu zakačene, \(1-n(x,t)\), i stope uspostavljanja veze, \(f(x)\). S druge strane, verovatnoća da se uspostavljena veza između aktina i miozina prekine je data kao \(n(x,t) g(x)\).

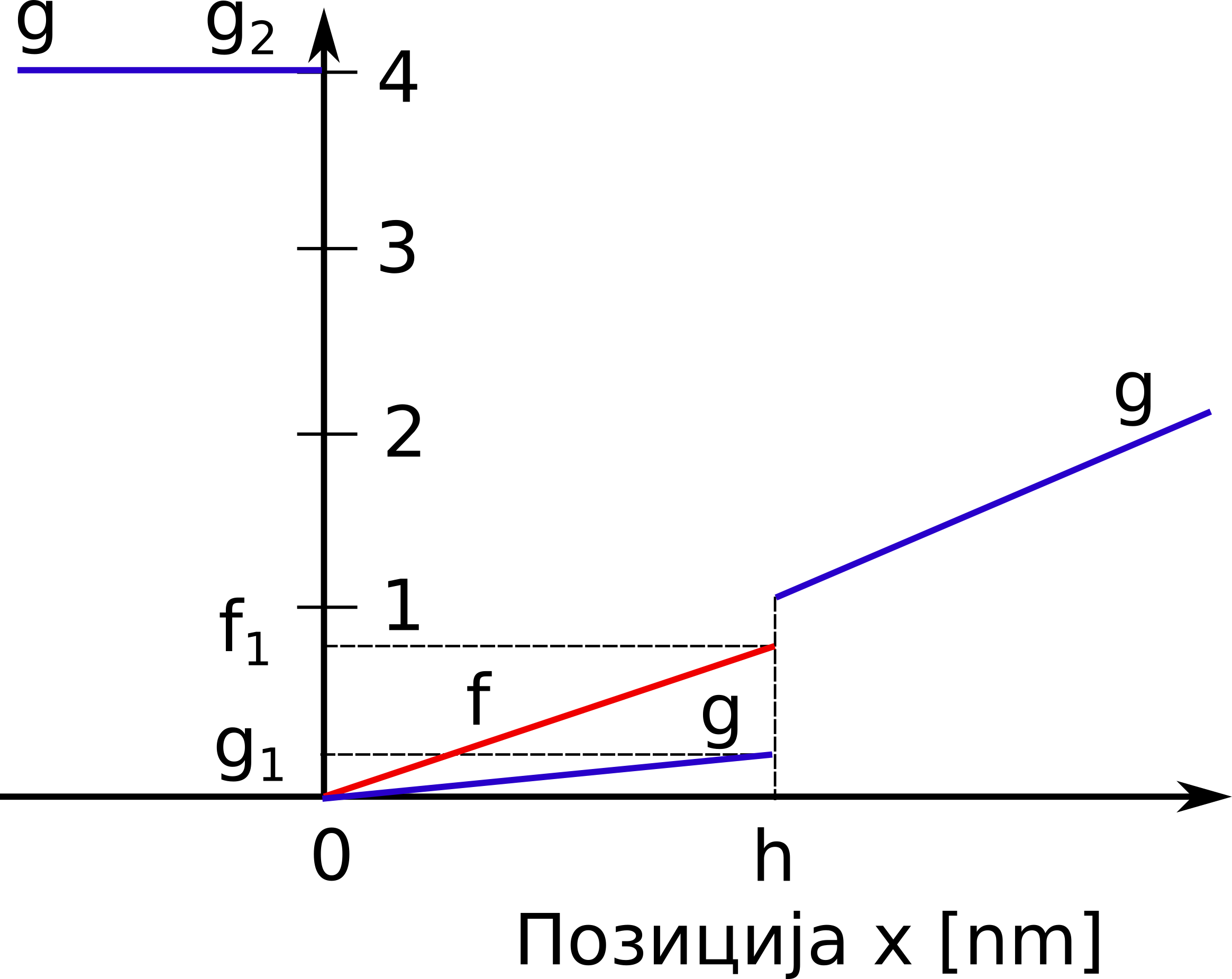
Sl. 46 Stope uspostavljanja veze, \(f\), (narandžasta linija) i raskidanja veze, \(g\), (plava linija) između miozina i aktina

Hakslijeva teorija kinetike poprečnih mostova se može izraziti korišćenjem parcijalne diferencijalne jednačine nad domenom \(\Omega\):

\[\frac{\partial n}{\partial t} (x,t) - v \frac{\partial n}{\partial x} = \mathcal{N} \left( n(x,t), x\right), \qquad \forall x \in \Omega,\]

gde je \(v= -dx/dt\) brzina klizanja filamenta aktina u odnosu na filament miozina (pozitivna pri kontrakciji), a

\[\mathcal{N} \left( n(x,t), x\right) = \left[ 1-n(x,t) \right] f(x) - n(x,t) g(x)\]

predstavlja brzinu promene stanja poprečnih mostova.

U cilju što realističnijeg opisa ponašanja mišića tokom izduženja, Zahalak je uveo određene modifikacije originalnog Hakslijevog modela. Uveo je minimalne promene u definiciji stopa uspostavljanja i raskidanja veza između miozina i aktina, tako da je pri skraćivanju mišića sve ostalo nepromenjeno, dok je pri izduženju omogućio veću stopu otkačinjanja. Ovo je praktično realizovano tako što je uveden Zahalakov faktor, \(f_{Zah}\), u slučaju kada je dužina poprečnog mosta \(x\) veća od \(h\):

(34)\[\begin{split}x<0 \quad : \quad f(x)=0; \, g(x)=g_2; \\ 0 \le x \le h \quad : \quad f(x)=f_1 x/h; \, g(x)=g_1 x/h; \\ x>h \quad : \quad f(x)=0; \, g(x)=f_{Zah} \, g_1 x / h\end{split}\]

Može se uočiti da je u oblasti \(x<0\) definisana visoka vrednost stope otkačinjanja, \(g(x)=g_2\) , kako bi se poprečni mostovi koji su dospeli u ovu zonu brzo prekinuli. Postoji izvesna stopa otkačinjanja i u oblasti \(0<x<h\), ali je niska u poređenju sa negativnom oblašću.

Nakon završene obuke neuronske mreže, ona se može koristiti kao zamena za metod karakteristika objašnjen u Svičević [Svivcevic20]. Ovde ćemo se zaustaviti sa objašnjavanjem matematičkog modela, a čitaoca koji se interesuje za izučavanje ove oblasti uputiti na Svičević [Svivcevic20].