Izometrijski slučaj

Radi testiranja sposobnosti NMPFZ da rešavaju ovu vrstu parcijalnih diferencijalnih jednačina, najpre je od interesa izometrijski slučaj, jer je on najjednostavniji, budući da je brzina klizanja filamenata jednaka nuli. Kod izometrijskog slučaja, višeslojni perceptron kao ulaz uzima poziciju \(x\) dostupnog aktinskig sajta u odnosu na ravnotežni položaj miozinske glave i vreme \(t\), a predviđa verovatnoće zakačinjanja miozinskih glava za aktinske sajtove \(n(x,t)\).

Implementacija

Kompletan kod je dat na sledećem listingu.

Listing 11 Rešenje Hakslijeve jednačine za izometrijski slučaj

import deepxde as dde
import numpy as np
import tensorflow as tf

''' fixed parameters '''
f1_0 = 43.3
h = 15.6
g1 = 10.0
g2 = 209.0
fzah = 4.0
a = 1.

# Verovatnoca kacenja
def f(x,a):
    return (1+tf.sign(x)) * (1-tf.sign(x-h)) * (f1_0*a*x/h) * 0.25

# Verovatnoca raskacivanja
def g(x):
    return 0.5 * (1-tf.sign(x)) * g2 + \
        0.25 * (1+tf.sign(x)) * (1-tf.sign(x-h)) * (g1*x/h) + \
        0.5 * (1+tf.sign(x-h)) * (fzah*g1*x/h)

# n = n(x,t)
def pde(x, n):
    dn_dt = dde.grad.jacobian(n, x, i=0, j=1)
    loss = dn_dt - (1.0-n) * f(x[:,0:1],a) + n*g(x[:,0:1])
    # Obezbedi pozitivna resenja
    return loss + n*(1-tf.sign(n))

# Computational geometry
geom = dde.geometry.Interval(-20.8, 63)
timedomain = dde.geometry.TimeDomain(0, 0.4)
geomtime = dde.geometry.GeometryXTime(geom, timedomain)

# Pocetni uslovi
ic1 = dde.icbc.IC(geomtime, lambda x: 0.0, lambda _, on_initial: on_initial)

data = dde.data.TimePDE(geomtime, pde, [ic1], num_domain=10000, num_boundary=100, num_initial=500)
net = dde.nn.FNN([2] + [40] * 3 + [1], "tanh", "Glorot normal")
model = dde.Model(data, net)

model.compile("adam", lr=1e-3)
model.train(100000)
model.compile("L-BFGS", loss_weights=[1.e-1, 1])
losshistory, train_state = model.train()
dde.saveplot(losshistory, train_state, issave=True, isplot=True)

Konstruisana je mreža sa 3 sloja, sa po 40 neurona i aktivacionom funkcijom tanh. Generisana je mreža podataka za 10.000 ekvidistantnih vrednosti za \(x\) u opsegu \(-20.8 [nm] \, \le x \le 63 \, [nm]\) i sa 500 nasumičnih vrednosti za \(t\) u opsegu \(0 \, [s] \le t \le 0.4 \, [s]\). Ove generisane tačke su korišćene kao ulazni podaci za obuku mreže. U toku obuke, od 100.000 epoha, minimizuje se rezidual Hakslijeve jednačine za mišićnu kontrakciju i rezidual početnog uslova, korišćenjem Adam optimizacije sa stopom učenja \(10^{-3}\).

Što se same implementacije tiče, treba skrenuti pažnju na nekoliko bitnih momenata. Kao prvo, da bismo formulisali jednačine (34) ne savetuje se korišćenje uslovih izraza (if klauzula), već se ista funkcionalnost interpretira pomoću TensorFlow izraza za znak, ako se on koristi kao bekend. Na primer:

def g(x):
    return 0.5 * (1-tf.sign(x)) * g2 + \
        0.25 * (1+tf.sign(x)) * (1-tf.sign(x-h)) * (g1*x/h) + \
        0.5 * (1+tf.sign(x-h)) * (fzah*g1*x/h)

U funkciji parcijalne diferencijalne jednačine imamo nešto drugačiji problem. Naime, moramo da obezbedimo da funkcija \(n(x,t)\) ne počne da uzima vrednosti manje od nule. Iako sama matematička postavka to dozvoljava, podsetimo se da \(n(x,t)\) označava verovatnoću zakačinjanja, pa negativna vrednost nema nikakvog fizičkog smisla. To ćemo uraditi na sledeći način:

def pde(x, n):
    dn_dt = dde.grad.jacobian(n, x, i=0, j=1)
    loss = dn_dt - (1.0-n) * f(x[:,0:1],a) + n*g(x[:,0:1])
    # Obezbedi pozitivna resenja
    return loss + n*(1-tf.sign(n))

U poslednjoj liniji se vrednosti funkcije gubitka dodaje član koji ima nenultu vrednost u slučaju da je \(n\) negativno. Na prvi pogled, bilo bi dovoljno umesto n*(1-tf.sign(n)) postaviti samo 1-tf.sign(n). Međutim, ispostavlja se da tako formirana funkcija gubitka ne dovodi do konvergencije, jer nije diferencijabilna, pa optimizacioni algoritmi kao što je Adam ne konvergiraju. Kada se pak funkcija znaka pomnoži sa \(n\), dobijamo diferencijabilniju funkciju gubitka, a samim tim i veću verovatnoću konvergencije.

Kao i u primeru Propagacija talasa u otvorenom kanalu, i ovde ćemo pokušati da dodatno smanjimo vrednost funkcije gubitka metodom L-BFGS:

model.compile("L-BFGS", loss_weights=[1.e-1, 1])
losshistory, train_state = model.train()

Veoma je važno ispoštovati postavljene početne uslove, pa ćemo im pomoću loss_weights=[1.e-1, 1] dati za red veličine veću težinu od komponente koja sledi iz same parcijalne diferencijalne jednačine.

Rezultati

I ovaj primer će usled velikog broja kolokacionih tačaka (podataka) najbolje performanse imati ukoliko se izvršava na nekom grafičkom procesoru koji ovu masovnost ume da paralelizuje. Na primer, na našem grafičkom procesoru NVidia Tesla T4 obuka traje oko 170 sekundi, dok na osmojezgarnom procesoru Intel Xeon Silver 4208 na 2.10GHz traje 2150 sekundi. To je ubrzanje od gotovo 13 puta!

Na Sl. 47 se vidi kako je tekao proces treninga NMPFZ. Uočljivo je da dodatno obučavanje pomoću L-BFGS definitivno ima efekta i da smo pomoću njega spustili vrednost gubitka za dodatni red veličine.

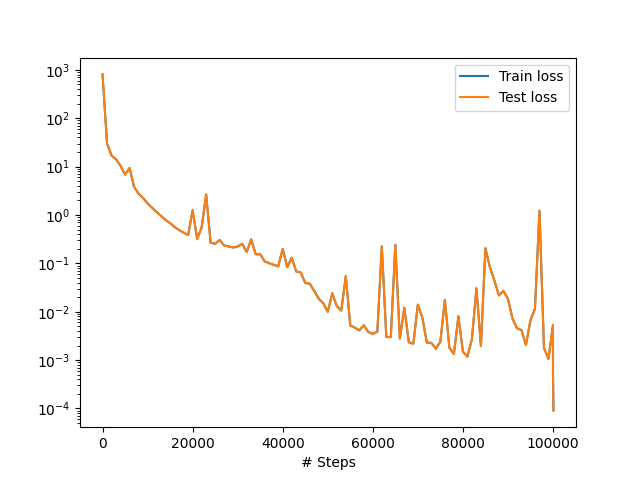
Sl. 47 Funkcija gubitka tokom obučavanja

Trodimenzionalni prikaz rezultata dat je na Sl. 48. Iz ovakvog prikaza nije pogodno utvrđivati bilo kakvu tačnost rešenja, ali je dovoljan za kvalitativni uvid. Uočljivo je da blizu \(t=0\) (\(x_2\) na slici) ima nekoliko kolokacionih tačaka gde je \(n(x,t)<0\), ali sveukupno rešenje deluje logično.

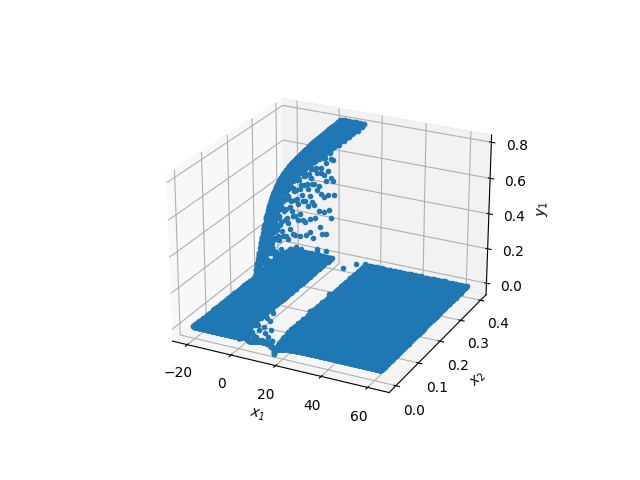
Sl. 48 Trodimenzionalni prikaz dobijenih rezultata. \(x_1\) je prostorna koordinata, a \(x_2\) vremenska.

Precizniju vizuelnu analizu rezultata možemo obaviti tek grafičkim predstavljanjem verovatnoće zakačinjanja mostova \(n(x,t)\) duž \(x\) ose u nekoliko različitih vremenskih trenutaka, kao što je dato na Sl. 49. Kao što smo očekivali, uočljiva je mala nestabilnost oko tačke \(x=h\) u nekoliko prvih vremenskih koraka, ali se ona gubi kako proces zakačinjanja napreduje.

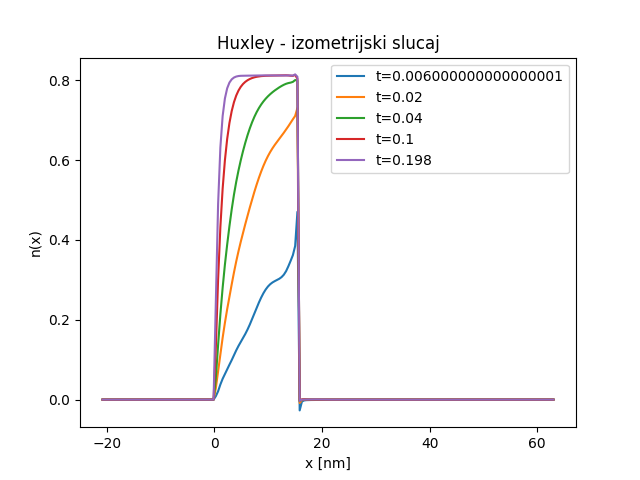
Sl. 49 Veličina \(n(x,t)\) u nekoliko različitih vremenskih trenutaka

Upoređivanje rezultata sa onima koji su dobijeni metodom karakteristika izlazi iz okvira ovog praktikuma, pa ćemo taj deo preskočiti. Na kraju je važno napomenuti da jednu potencijalnu primenu NMPFZ na koju do sada nismo obraćali pažnju, a može biti od velike koristi. Naime, dok kod klasičnih numeričkih metoda za rešavanje parcijalnih diferencijalnih jednačina, rešenje u vremenskom koraku \(m+1\) zavisi od rešenja koje smo imali u vremenskom koraku \(m\). Kod svih primera koje smo obradili pomoću NMPFZ to nije slučaj, jer se vreme uzima kao bilo koja druga promenljiva po kojoj se vrši parcijalna diferencijacija. Ako pogledamo Sl. 49 očigledno je da u trenutku \(t=0,006\) imamo grešku. Međutim, ta greška se ne propagira na kasnije vremenske trenutke baš iz navedenog razloga.

Ovaj drugačiji tretman vremena kao ulazne promenljive ima implikacije i na performanse. Naime, kada se NMPFZ model koristi u produkciji, i potrebno nam je da znamo npr. \(n(x,t=t_1)\) nije potrebno da prođemo kroz sve vremenske korake \(t \le t_1\), već odmah možemo da izbacimo rezultat, jednim prolaskom kroz obučenu NMPFZ. Time se vreme značajno štedi i za nekoliko redova veličine. Time se otvaraju neke nove primene, naročito u oblasti modelovanja na više skala, kao na primer u Svičević [Svivcevic20]. Takvim skokom u performansama bilo bi moguće ovakve složene modele izvoditi skoro u realnom vremenu.