Решавање на домену облика квадрата

Кренућемо од најједноставнијег дводимензионог случаја стојећег таласа у акустици. За таласни број \(k_0=2 \pi n\) за \(n=2\), треба решити Хелмхолцову (Helmholtz) једначину облика:

\[-\frac{\partial^2 u}{\partial x^2} - \frac{\partial^2 u}{\partial y^2} - k_0^2 u = f, \quad \Omega=[0,1]^2,\]

уз Дирихлеове граничне услове

\[u(x,y)=0, \quad (x,y) \in \partial \Omega\]

приказане на Сл. 37 и члан који специфицира извор \(f(x,y)=k_0^2 \sin(k_0x) \sin(k_0 y)\).

../_images/akustika1.png

Сл. 37 Поставка проблема и гранични услови.

Постоји аналитичко решење овог проблема и оно гласи:

\[u(x,y) = \sin(k_0 x) \sin(k_0 y).\]

За више детаља у погледу теоријске позадине диференцијалне једначине и граничних услова читалац може консултовати Ihlenburg [Ihl98]. Решење методом коначних елемената (МКЕ) је такође доступно у оквиру Dolfinx туторијала.

Имплементација

Решење директног проблема приказано је на следећем листингу.

Листинг 8 Решење проблема простирања стојећег таласа у 2Д коришћењем DeepXDE библиотеке
 1import deepxde as dde
 2import numpy as np
 3
 4# Frekvencija
 5n = 2
 6
 7precision_train = 10
 8precision_test = 30
 9weights = 100
10iterations = 10000
11learning_rate, num_dense_layers, num_dense_nodes, activation = 1e-3, 3, 150, "sin"
12
13# Uvezi sinus
14from deepxde.backend import tf
15sin = tf.sin
16
17# Osnovna PDE
18def pde(x, u):
19    du_xx = dde.grad.hessian(u, x, i=0, j=0)
20    du_yy = dde.grad.hessian(u, x, i=1, j=1)
21
22    f = k0 ** 2 * sin(k0 * x[:, 0:1]) * sin(k0 * x[:, 1:2])
23    return -du_xx - du_yy - k0 ** 2 * u - f
24
25# Egzaktno resenje
26def func(x):
27    return np.sin(k0 * x[:, 0:1]) * np.sin(k0 * x[:, 1:2])
28
29# Da li je kol. tacka na granici?
30def boundary(_, on_boundary):
31    return on_boundary
32
33# Geometrija jedinicnog kvadrata
34geom = dde.geometry.Rectangle([0, 0], [1, 1])
35# Talasni broj
36k0 = 2 * np.pi * n
37# Talasna duzina
38wave_len = 1 / n
39
40hx_train = wave_len / precision_train
41nx_train = int(1 / hx_train)
42
43hx_test = wave_len / precision_test
44nx_test = int(1 / hx_test)
45
46# Dirihleov granicni uslov y=0 na granicama
47bc = dde.icbc.DirichletBC(geom, lambda x: 0, boundary)
48
49data = dde.data.PDE(
50    geom,
51    pde,
52    bc,
53    num_domain=nx_train ** 2,
54    num_boundary=4 * nx_train,
55    solution=func,
56    num_test=nx_test ** 2,
57)
58
59# Mreza i model
60net = dde.nn.FNN([2] + [num_dense_nodes] * num_dense_layers + [1], activation, "Glorot uniform")
61model = dde.Model(data, net)
62
63# Forsiraj vece tezine za granicne uslove nego za unutrasnjost domena
64loss_weights = [1, weights]
65
66model.compile("adam", lr=learning_rate, metrics=["l2 relative error"], loss_weights=loss_weights)
67
68losshistory, train_state = model.train(iterations=iterations)
69dde.saveplot(losshistory, train_state, issave=True, isplot=True)

Након стандардног импорта одговарајућих модула, почињемо спецификацијом општих параметара. Овај пример има пар специфичности у односу на остале. Наиме, да би се успешно моделовале таласне појаве помоћу НМПФЗ, густина колокационих тачака мора да буде директно пропорционална фреквенцији. Што је виша фреквенција n, мања је таласна дужина wave_len, па је потребно више колокационих тачака да покрије домен. Овде смо узели 10 колокационих тачака по таласној дужини током тренинга и 30 тачака по таласној дужини у тест скупу.

# Frekvencija talasa
n = 2
precision_train = 10
precision_test = 30
weights = 100
learning_rate, num_dense_layers, num_dense_nodes, activation = 1e-3, 3, 150, "sin"

Такође, видимо да користимо архитектуру са мањим бројем слојева, али са више неурона по слоју, као и активациону функцију \(\sin(x)\) која би требало да буде погоднија за опонашање таласних феномена.

Следи спецификација саме парцијалне диференцијалне једначине у облику функције губитка како смо то већ навикли:

def pde(x, u):
    du_xx = dde.grad.hessian(u, x, i=0, j=0)
    du_yy = dde.grad.hessian(u, x, i=1, j=1)

    f = k0 ** 2 * sin(k0 * x[:, 0:1]) * sin(k0 * x[:, 1:2])
    return -du_xx - du_yy - k0 ** 2 * u - f

Овде користимо услужну функцију dde.grad.hessian одабиром координате која се диференцира и којом се диференцира. У овом примеру су гранични услови елементарни, па их овде нећемо посебно наводити.

Геометрија, таласни број \(k_0=2 \pi \nu\) и таласна дужина \(\lambda=\frac{1}{\nu}\) дају се као:

geom = dde.geometry.Rectangle([0, 0], [1, 1])
k0 = 2 * np.pi * n
wave_len = 1 / n

Једина специфичност коју додатно треба нагласити је да понекад треба форсирати поштовање граничних услова тиме што ћемо члану функције губитка који се односи на Дирихлеов гранични услов добити већу тежину у односу на члан који се односи на диференцијалну једначину.

weights = 100
loss_weights = [1, weights]
model.compile("adam", lr=learning_rate, metrics=["l2 relative error"], loss_weights=loss_weights)

Да би се избегао овај корак који са собом носи експериментисање са различитим вредностима тежинског фактора, гранични услов се код DeepXDE може задавати и директном трансформацијом функције губитка, али овде се тиме нећемо бавити.

Резултати

Након 10.000 епоха обучавања оптимизационом методом Adam који је протекао као што је приказано на Сл. 38, добијамо стојећи талас чији 3Д приказ можемо видети на Сл. 39.

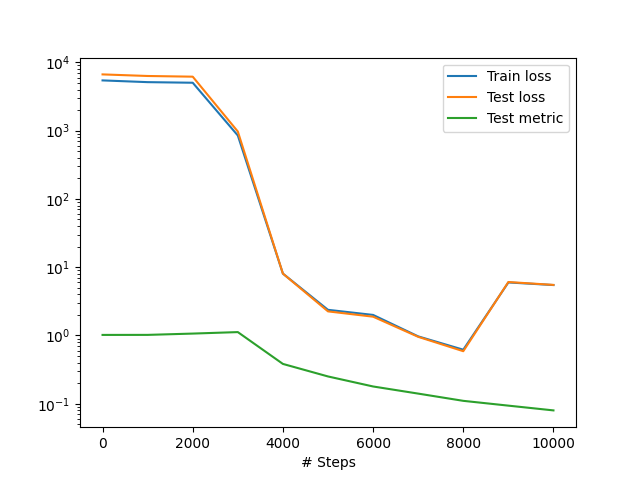
../_images/rezultati1-loss.png

Сл. 38 Ток обучавања НМПФЗ

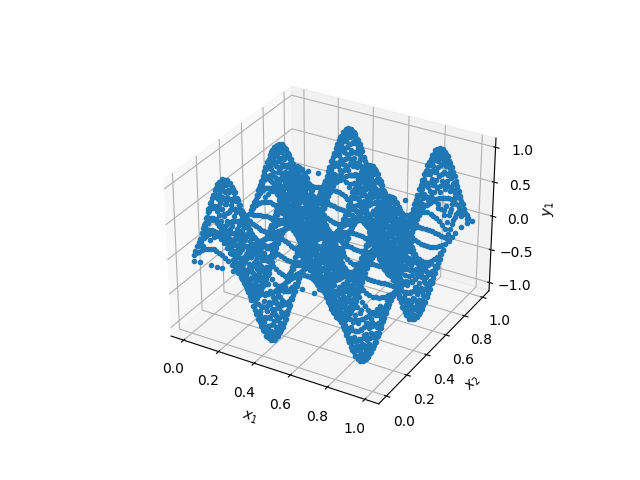
../_images/rezultati1.png

Сл. 39 Тродимензиони приказ таласа у домену облика квадрата

Мера грешке модела RMSE (Root Mean Squared Error) износи \(7,98 \cdot 10^{-2}\). Уз обраћање посебне пажње на форсирање граничних услова, затим архитектуру НМПФЗ и најзад тип активационе функције, успели смо да добијемо прилично добро решење. Читалац може самостално да проба како би промена фреквенције (а самим тим и таласне дужине), густине колокационих тачака, архитектуре, утицала на процес обучавања модела.

Овде можемо дати и кратку препоруку како приступити моделовању сложенијих појава, са сложенијом геометријом и комплекснијим граничним условима. Пошто НМПФЗ решавање зависи од већег броја хипер-параметара, препорука је да се прво реши до краја поједностављен проблем базиран на истој диференцијалној једначини, али са једноставнијом геометријом и граничним условима. Када се стекне слика о томе која комбинација хипер-параметара води до конвергенције решења, онда је лакше приступити главном, комплексном проблему. С друге стране, постоји неколико алата који претрагу хипер-параметара чине ефикаснијом, као већ поменути BlackFox који користи дистрибуирани генетски алгоритам.