Решавање на домену облика квадрата са шупљином

У односу на претходни пример Решавање на домену облика квадрата додајемо шупљину у средини квадратног домена и прописујемо одговарајуће Нојманове граничне услове на ободу шупљине. Да се подсетимо, домен проблема \(\Omega\) је квадрат странице \(L, \, L=1\), из кога искључујемо круг полупречника \(R=\frac{1}{4}\). За таласни број \(k_0=2 \pi n\) и \(n=1\), решавамо Хелмхолцову једначину:

\[-\frac{\partial^2 u}{\partial x^2} - \frac{\partial^2 u}{\partial y^2} - k_0^2 u = f, \quad \text{ u } \Omega,\]

где је члан који специфицира извор \(f(x,y)=k_0^2 \sin(k_0x) \sin(k_0 y)\). Облик домена може се видети на Сл. 40.

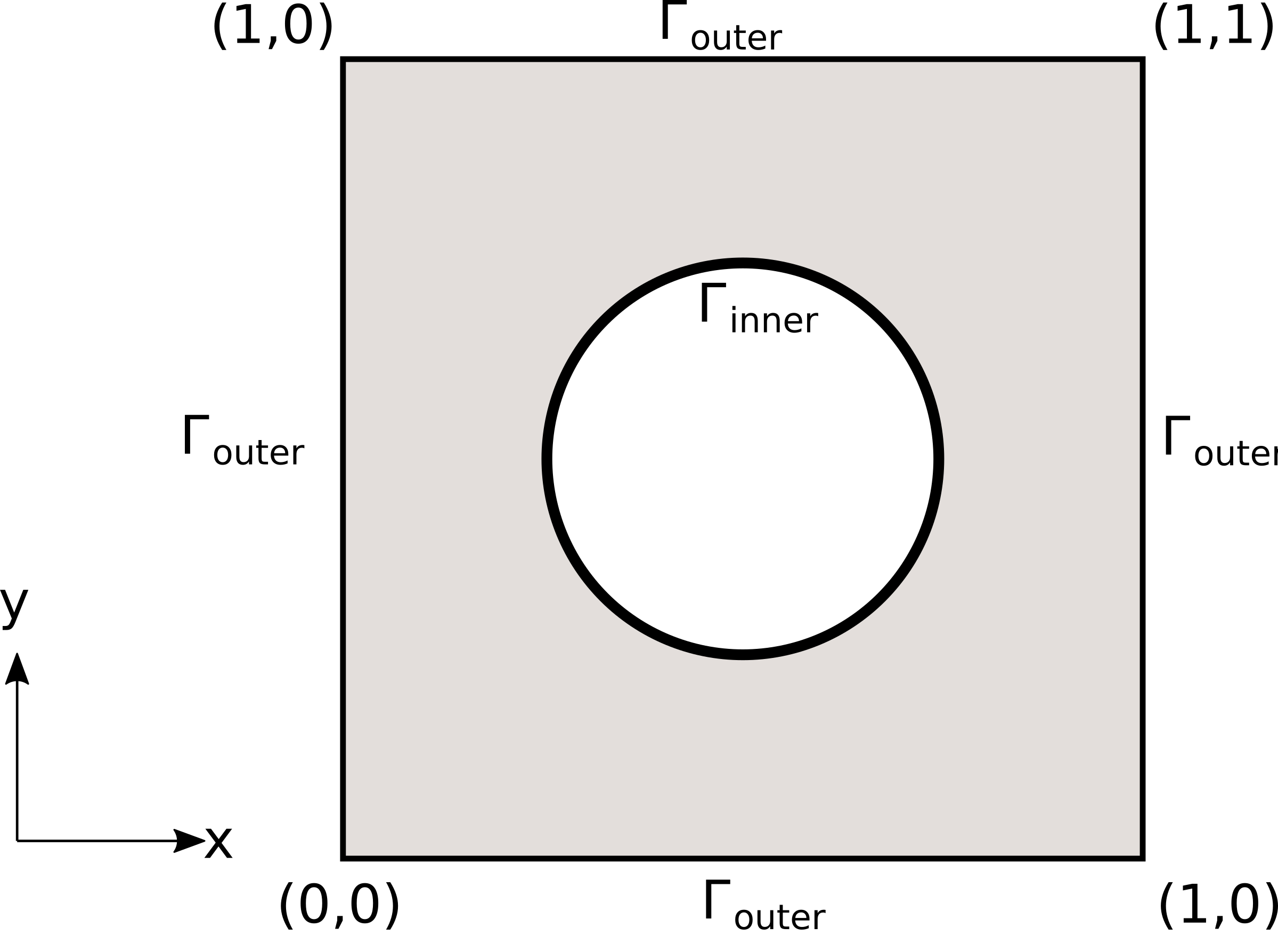
../_images/akustika2.png

Сл. 40 Поставка проблема и гранични услови

Постоји аналитичко решење овог проблема и оно гласи:

\[u(x,y) = \sin(k_0 x) \sin(k_0 y).\]

Овде ћемо специфицирати Дирихлеове граничне услове према аналитичком решењу на спољној граници домена \(\Omega\) коју означавамо са \(\Gamma_{outer}\):

\[u(x,y) \left| \right. \Gamma_{outer} = \sin(k_0 x) \sin(k_0 y), \quad (x,y) \in \Gamma_{outer}\]

На сличан начин, можемо да дефинишемо гранични услов на унутрашњој граници, овог пута Нојманов:

(30)\[(\nabla u \left| \right. \Gamma_{inner} \cdot n) (x,y) = \left[ k_0 \cos(k_0 x) \sin(k_0 y), k_0 \sin(k_0 x) \cos(k_0 y) \right] \cdot n = g(x,y),\]

где је \(n\) вектор нормале. Концизније написано, Нојманов гранични услов на унутрашњој граници гласи:

\[\nabla u \left| \right. \Gamma_{inner} \cdot n = g.\]

Имплементација

На следећем листингу су дати главни детаљи имплементације. Намерно су изостављени делови који су ирелевантни за само решавање, као што је цртање дијаграма. Целокупна скрипта се, као и остале, налази у репозиторијуму са примерима.

Листинг 9 Решење проблема простирања стојећег таласа у 2Д домену са шупљином
 1import deepxde as dde
 2import matplotlib.pyplot as plt
 3import numpy as np
 4from deepxde.backend import tf
 5sin = tf.sin
 6
 7# Opsti parametri
 8n = 2
 9length = 1
10R = 1 / 4
11
12precision_train = 15
13precision_test = 30
14
15weight_inner = 10
16weight_outer = 100
17iterations = 5000
18learning_rate = 1e-3
19num_dense_layers = 3
20num_dense_nodes = 350
21activation = "sin"
22
23k0 = 2 * np.pi * n
24wave_len = 1 / n
25
26# Parcijalna diferencijalna jednacina
27def pde(x, y):
28    dy_xx = dde.grad.hessian(y, x, i=0, j=0)
29    dy_yy = dde.grad.hessian(y, x, i=1, j=1)
30    f = k0**2 * sin(k0 * x[:, 0:1]) * sin(k0 * x[:, 1:2])
31    return -dy_xx - dy_yy - k0**2 * y - f
32
33# Egzaktno resenje
34def func(x):
35    return np.sin(k0 * x[:, 0:1]) * np.sin(k0 * x[:, 1:2])
36
37# Da li je tacka na granici?
38def boundary(_, on_boundary):
39    return on_boundary
40
41# Njumanovi granicni uslovi prema egzaktnom resenju
42def neumann(x):
43    grad = np.array([
44            k0 * np.cos(k0 * x[:, 0:1]) * np.sin(k0 * x[:, 1:2]),
45            k0 * np.sin(k0 * x[:, 0:1]) * np.cos(k0 * x[:, 1:2]),])
46
47    normal = -inner.boundary_normal(x)
48    normal = np.array([normal]).T
49    result = np.sum(grad * normal, axis=0)
50    return result
51
52# Geometrija
53outer = dde.geometry.Rectangle([-length / 2, -length / 2], [length / 2, length / 2])
54inner = dde.geometry.Disk([0, 0], R)
55
56# Da li je tacka na spoljnoj granici?
57def boundary_outer(x, on_boundary):
58    return on_boundary and outer.on_boundary(x)
59
60# Da li je tacka na unutrasnjoj granici?
61def boundary_inner(x, on_boundary):
62    return on_boundary and inner.on_boundary(x)
63
64# Iskljuci krug iz kvadrata
65geom = outer - inner
66
67hx_train = wave_len / precision_train
68nx_train = int(1 / hx_train)
69
70hx_test = wave_len / precision_test
71nx_test = int(1 / hx_test)
72
73# Na unutrasnjoj granici Njuman, na spoljnoj Dirihleovi
74bc_inner = dde.icbc.NeumannBC(geom, neumann, boundary_inner)
75bc_outer = dde.icbc.DirichletBC(geom, func, boundary_outer)
76
77data = dde.data.PDE(
78    geom,
79    pde,
80    [bc_inner, bc_outer],
81    num_domain=nx_train**2,
82    num_boundary=16 * nx_train,
83    solution=func,
84    num_test=nx_test**2,
85)
86
87net = dde.nn.FNN(
88    [2] + [num_dense_nodes] * num_dense_layers + [1], activation, "Glorot uniform"
89)
90
91model = dde.Model(data, net)
92
93loss_weights = [1, weight_inner, weight_outer]
94model.compile("adam", lr=learning_rate, metrics=["l2 relative error"], loss_weights=loss_weights)
95
96losshistory, train_state = model.train(iterations=iterations)

Користићемо Tensorflow као backend у свим нашим примерима, али треба имати у виду да оквир DeepXDE подржава и PyTorch и још неке. Након стандардне спецификације општих параметара и хипер-параметара, као у примеру Решавање на домену облика квадрата, уз једину модификацију додавања нешто више неурона по слоју (350), дефинишемо Нојманов гранични услов према једначини (30):

def neumann(x):
    grad = np.array([
            k0 * np.cos(k0 * x[:, 0:1]) * np.sin(k0 * x[:, 1:2]),
            k0 * np.sin(k0 * x[:, 0:1]) * np.cos(k0 * x[:, 1:2]),])

    normal = -inner.boundary_normal(x)
    normal = np.array([normal]).T
    result = np.sum(grad * normal, axis=0)
    return result

Као што се види из кода, постоје услужне функције које рачунају нормале на правилне границе у колокационим тачкама. Пондерске тежине граничних услова у обуци weight_inner и weight_outer такође спадају у неку врсту хипер-параметара, па и њима треба посветити пажњу уз неколико мануелних проба. Даље, следи спецификација геометрије проблема као разлике квадрата и диска:

outer = dde.geometry.Rectangle([-length / 2, -length / 2], [length / 2, length / 2])
inner = dde.geometry.Disk([0, 0], R)
geom = outer - inner

Остатак скрипте је сличан примеру без шупљине Решавање на домену облика квадрата, па га нећемо додатно појашњавати. Довољно је рећи да пажњу треба обратити да буде довољно колокационих тачака на спољној и на унутрашњој граници.

Резултати

Добијени резултати су приказани у форми контурног графика на Сл. 41. Око унутрашње границе приказани су правци вектора нормала.

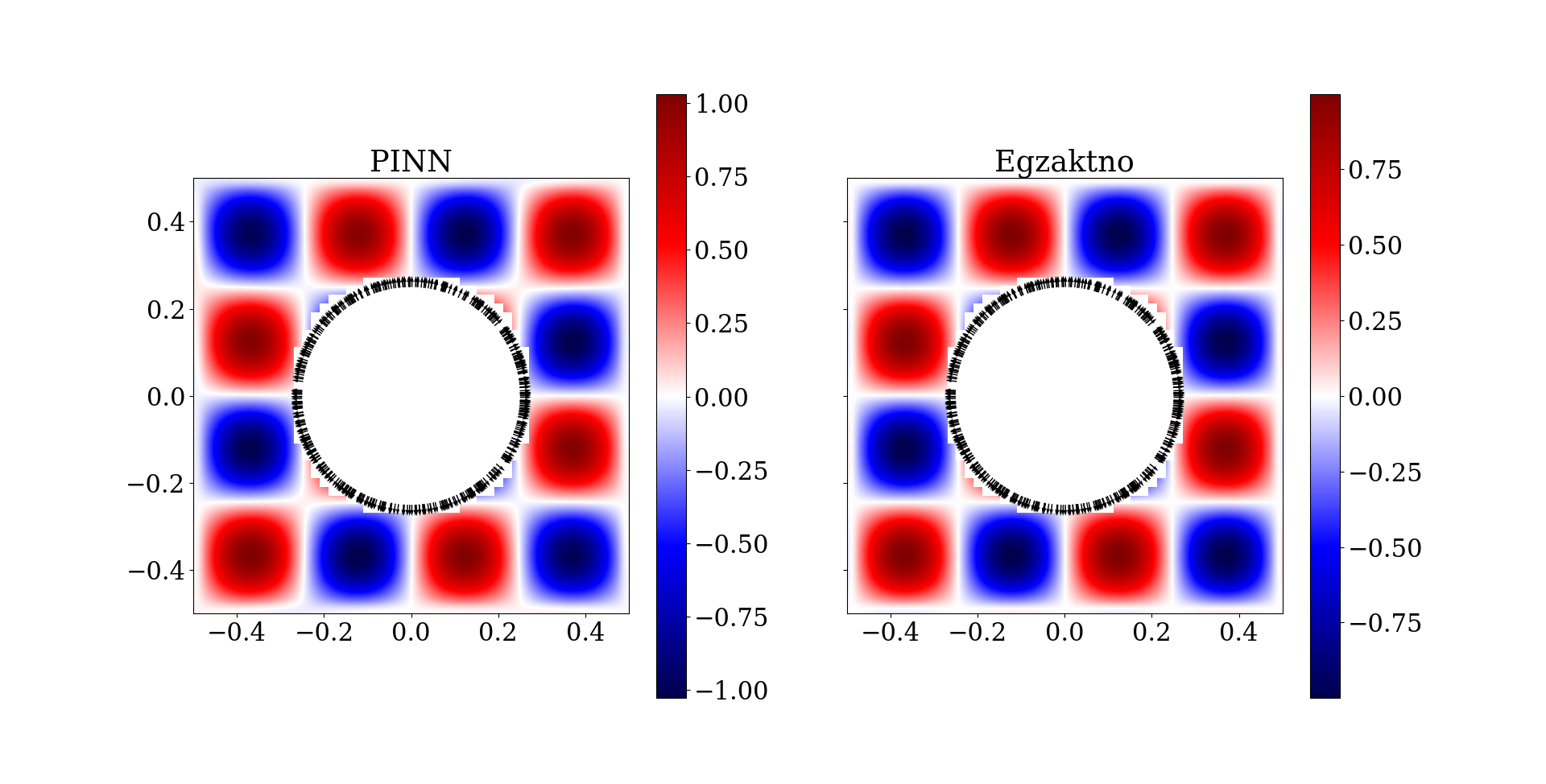
../_images/rezultati-rupa.png

Сл. 41 Резултати примера квадратног домена са шупљином

Мера релативне грешке модела износи 0,048. Уз обраћање посебне пажње на форсирање граничних услова, затим архитектуру НМПФЗ и најзад тип активационе функције, успели смо да добијемо прилично добро решење. Читалац може самостално да проба како би промена фреквенције (а самим тим и таласне дужине), густине колокационих тачака, архитектуре, утицала на процес обуке модела.