Дводимензиони проблем са сочивом
Овај одељак се бави нешто модификованим примером из туторијала за познати софтверски оквир за рад са методом коначних елемената Deal.II. Првобитна сврха овог примера је да симулира својства фокусирања ултразвучног таласа који генерише сочиво претварача са променљивом геометријом. Савремене примене у медицинском имиџингу користе ултразвучне таласе не само за сврхе снимања, већ и за изазивање одређених локалних ефеката у материјалу, као што су промене у оптичким својствима, које се затим могу мерити другим техникама снимања. Витални састојак ових метода је способност фокусирања интензитета ултразвучног таласа у одређеном делу материјала, идеално у тачки, како би се могла испитати својства материјала на тој локацији.
Карактеристична таласна дужина ултразвука нешто мања од феномена које смо до сада моделовали методом НМПФЗ, те би нам био потребан изузетно велики број колокационих тачака што продужава тренирање. Зато смо таласну дужину нешто повећали (смањили фреквенцију), док остале параметре нисмо мењали.
Како бисмо извели једначине за овај проблем, звук узимамо као талас којим се шири промена притиска:
где је \(c\) брзина звука, која се због једноставности узима као константа, \(U = U(x,t) ,\; x \in \Omega, \; t \in \mathrm{R}\). Поставка проблема дата је на Сл. 42.

Сл. 42 Поставка проблема и гранични услови
Граница \(\Gamma=\partial\Omega\) подељена је на два дела, и то \(\Gamma_1\) и \(\Gamma_2 = \Gamma\setminus\Gamma_1\), где \(\Gamma_1\) представља сочиво, а \(\Gamma_2\) апсорбујућу границу. Заправо, желимо да направимо такав гранични услов на \(\Gamma_2\) тако да се опонаша знатно већи домен. На \(\Gamma_1\), претварач генерише таласе константне фреквенције \(\omega > 0\) и константне јединичне амплитуде:
Пошто нема других (интерних или граничних) извора и пошто само извор емитује таласе фреквенције \(\omega\), дозвољено је да извршимо раздвајање променљивих \(U(x,t) = \textrm{Re}\left(u(x)\,e^{i\omega t})\right)\). Комплексна функција \(u(x)\) описује просторну зависност амплитуде и фазе (релативно у односу на извор) таласа фреквенције \(\omega\), док је амплитуда величина која нас интересује. Ако овако формулисану функцију уврстимо у таласну једначину, видимо да за \(u\) имамо
Да бисмо нашли одговарајуће граничне услове на \(\Gamma_2\) који опонашају апсорбујућу границу, размотримо талас облика \(V(x,t)=e^{i(k\cdot x - \omega t)}\) фреквенције \(\omega\) који се простире у правцу \(k \in {\mathrm{R}^2}\). Да би \(V\) био решење таласне једначине, мора да важи \(|k|=\frac{\omega}{c}\). Претпоставимо да талас долази до \(x_0 \in \Gamma_2\) под правим углом, на пример \(n=\frac{k}{|k|}\) где \(n\) означава нормалу на \(\Omega \in x_0\). Онда у \(x_0\), овај талас задовољава једначину
Постављањем граничног услова
таласи који ударају у границу \(\Gamma_2\) под правим углом биће савршено апсорбовани. Са друге стране, они делови таласног поља који не падају под правим углом не задовољавају овај услов, па ће долазити до парцијалних рефлексија. У основи, директни делови таласа ће проћи кроз границу као да она не постоји, док ће остали бити рефлектовани назад у домен.
Уколико смо спремни да прихватимо овако предложену апроксимацију, онда за \(u\) важи следеће:
препознајемо Хелмхолцову једначину са Дирихлеовим условом на \(\Gamma_1\) и мешаним граничним условом на \(\Gamma_2\). Због услова на \(\Gamma_2\) не можемо да третирамо реалне и имагинарне делове \(u\) посебно. Оно што можемо да урадимо је да формирамо систем од две парцијалне диференцијалне једначине у којима фигуришу реални и имагинарни део \(u\), са граничним условима на \(\Gamma_2\) које везују ове две компоненте. Ако означимо да је \(v=\textrm{Re}\;u,\; w=\textrm{Im}\;u\), систем (31) гласи:
Дакле, прве две једначине важе у целом домену \(\Omega\), друге две на граници \(\Gamma_2\), а последње две на \(\Gamma_1\). Овде први пут имамо систем диференцијалних једначина, али ни то не би требало да буде проблем за НМПФЗ приступ, ако подразумевамо да је систем затворен, тј. једнозначан.
Имплементација
На основу система једначина (32) треба да формирамо композитну функцију губитка, да формирамо НМПФЗ мрежу и да је истренирамо на довољном броју колокационих тачака. Ево кључних делова имплементације остварене помоћу оквира SCIANN:
1import numpy as np
2import matplotlib.pyplot as plt
3import sciann as sn
4from numpy import pi
5from sciann.utils.math import diff, sign, sin, sqrt
6
7# Brzina talasa
8c = 1
9# Frekvencija
10omega = 2*pi*4
11
12x = sn.Variable('x')
13y = sn.Variable('y')
14v, w = sn.Functional (["v", "w"], [x, y], 3*[200] , 'sin')
15
16# Diferencijalne jednacine za v i w
17L1 = -omega**2 * v - c**2 * diff(v, x, order=2) - c**2 * diff(v, y, order=2)
18L2 = -omega**2 * w - c**2 * diff(w, x, order=2) - c**2 * diff(w, y, order=2)
19
20TOL = 0.015
21
22# Dirihleov uslov na G1 (y=0 i 0.4<x<0.6)
23a,b,c,d = 0.39762422, -1.57715550, -0.03696364, 1.60337246
24C1 = (1 - sign(y - (a + b*x + c*sqrt(x) + d*x**2 + TOL))) * (1 + sign(x-0.4)) * (1 - sign(x-0.6)) * (1-v)
25C2 = (1 - sign(y - (a + b*x + c*sqrt(x) + d*x**2 + TOL))) * (1 + sign(x-0.4)) * (1 - sign(x-0.6)) * (w-0)
26
27# Gornja granica G2 (gde je y=1)
28C3 = (1+sign(y - (1-TOL))) * ( c*diff(v,y) - omega*w )
29C4 = (1+sign(y - (1-TOL))) * ( c*diff(w,y) + omega*v )
30
31# Desna granica G2 (gde je x=1)
32C5 = (1+sign(x - (1-TOL))) * ( c*diff(v,x) - omega*w )
33C6 = (1+sign(x - (1-TOL))) * ( c*diff(w,x) + omega*v )
34
35# Leva granica G2 (gde je x=0)
36C7 = (1-sign(x - (0+TOL))) * ( -c*diff(v,x) - omega*w )
37C8 = (1-sign(x - (0+TOL))) * ( -c*diff(w,x) + omega*v )
38
39# Donja granica G2 (gde je y=0) i (x<0.4 or x>0.6)
40C9 = (1-sign(y - (0+TOL))) * ( (1 - sign(x-0.4)) + (1 + sign(x-0.6)) ) * ( -c*diff(v,y) - omega*w )
41C10 = (1-sign(y - (0+TOL))) * ( (1 - sign(x-0.4)) + (1 + sign(x-0.6)) ) * ( -c*diff(w,y) + omega*v )
42
43x_data, y_data = [], []
44
45kolokacione_tacke = np.genfromtxt('kolokacione_tacke.txt', delimiter=" ")
46
47for e in kolokacione_tacke:
48 ind, x1, y1 = e
49 x_data.append(x1)
50 y_data.append(y1)
51
52x_data, y_data = np.array(x_data), np.array(y_data)
53
54# Model i obucavanje
55m = sn.SciModel([x, y], [L1,L2,C1,C2,C3,C4,C5,C6,C7,C8,C9,C10], 'mse', 'Adam')
56h = m.train([x_data, y_data], 12*['zero'], learning_rate=0.001, batch_size=1024, epochs=8000, adaptive_weights={'method':'NTK', 'freq':200})
57
58# Test
59x_test, y_test = np.meshgrid(
60 np.linspace(0, 1, 200),
61 np.linspace(0, 1, 200)
62)
63v_pred = v.eval(m, [x_test, y_test])
64w_pred = w.eval(m, [x_test, y_test])
Након уобичајених импорта пакета, формирамо НМПФЗ мреже за реални део \(v\) и имагинарни део \(w\) непознате функције \(u\). И овде ћемо ићи са активационом функцијом \(\sin(x)\). Интересантан део кода је дефинисање граничног услова на \(\Gamma_1\) према последње две једначине у систему (32):
a,b,c = 0.39762422, -1.57715550, 1.60337246
C1 = (1 - sign(y - (a + b*x + c*x**2 + TOL))) * (1 + sign(x-0.4)) * (1 - sign(x-0.6)) * (1-v)
C2 = (1 - sign(y - (a + b*x + c*x**2 + TOL))) * (1 + sign(x-0.4)) * (1 - sign(x-0.6)) * (w-0)
Једначина \(y = a + b \cdot x + c \cdot x^2\) представља једначину спољне линије сочива \(\Gamma_1\), у којој су коефицијенти \(a,b,c\) добијени фитовањем. Дакле, прва заграда у граничним условима значи да узимамо колокационе тачке које припадају танком појасу изнад линије \(\Gamma_1\), док друга и трећа заграда имају ненулту вредност само ако је \(0,4 < x < 0,6\).
Гранични услови C3, C4, C5, C6, C7, C8 се односе на мешану формулацију према друге две једначине у систему (32) и важе на \(\Gamma_2\). На пример:
C5 = (1+sign(x - (1-TOL))) * ( c*diff(v,x) - omega*w )
C6 = (1+sign(x - (1-TOL))) * ( c*diff(w,x) + omega*v )
се односи на десну границу где је x=1 и узима колокационе тачке које се налазе у танком појасу ширине TOL са леве стране те границе.
Компоненте функције губитка C9 и C10 односе се такође на границу \(\Gamma_2\), али на линији где је \(y=0`\) и \(x < 0,4\) или \(x > 0,6\):
C9 = (1-sign(y - (0+TOL))) * ( (1 - sign(x-0.4)) + (1 + sign(x-0.6)) ) * ( -c*diff(v,y) - omega*w )
C10 = (1-sign(y - (0+TOL))) * ( (1 - sign(x-0.4)) + (1 + sign(x-0.6)) ) * ( -c*diff(w,y) + omega*v )
Овим смо комплетирали свих 12 компоненти функције губитка. Пошто их има толико, није једноставно извршити њихово пондерисање, односно доделу тежина свакој компоненти. У оваквим ситуацијама помажу методе за адаптивно одређивање тежина компоненти током обуке. У нашем решењу:
h = m.train([x_data, y_data], 12*['zero'], learning_rate=0.001, batch_size=1024, epochs=8000, adaptive_weights={'method':'NTK', 'freq':200})
употребили смо иновативну методу Neural Tangent Kernel (NTK) према Wang et al. [WYP22]. Објашњење методе излази из оквира овог практикума, па је нећемо детаљно разрађивати. Такође, ваља напоменути да смо колокационе тачке учитали из посебног фајла kolokacione_tacke.txt, који је добијен тако што смо исписали чворове коначних елемената који се добијају из генератора мреже пакета Deal.II.
Резултати
Као што је на почетку одељка већ речено, пример је преузет из документације за пакет који се бави анализом методом коначних елемената Deal.II, тако да можемо да упоредимо решење за \(v=\textrm{Re}\;u\) које смо добили помоћу НМПФЗ (Сл. 43) и решење које се добија класичном методом коначних елемената (Сл. 44). Решење добијено МКЕ методом можемо сматрати референтним, јер је коришћена веома густа мрежа и показана је конвергенција.
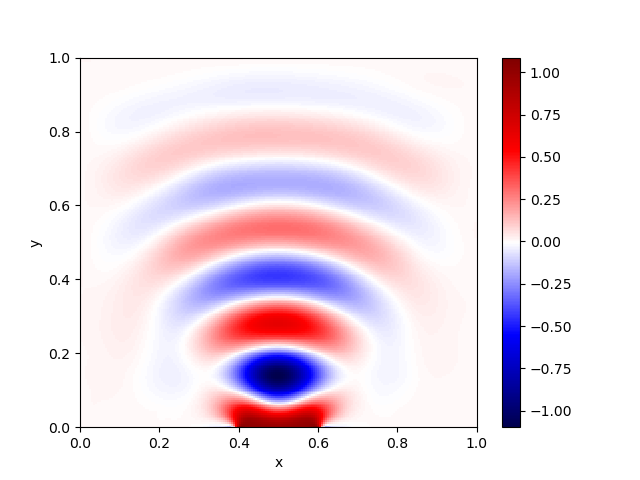
Сл. 43 Решење за \(v=\textrm{Re}\;u\) добијено помоћу НМПФЗ
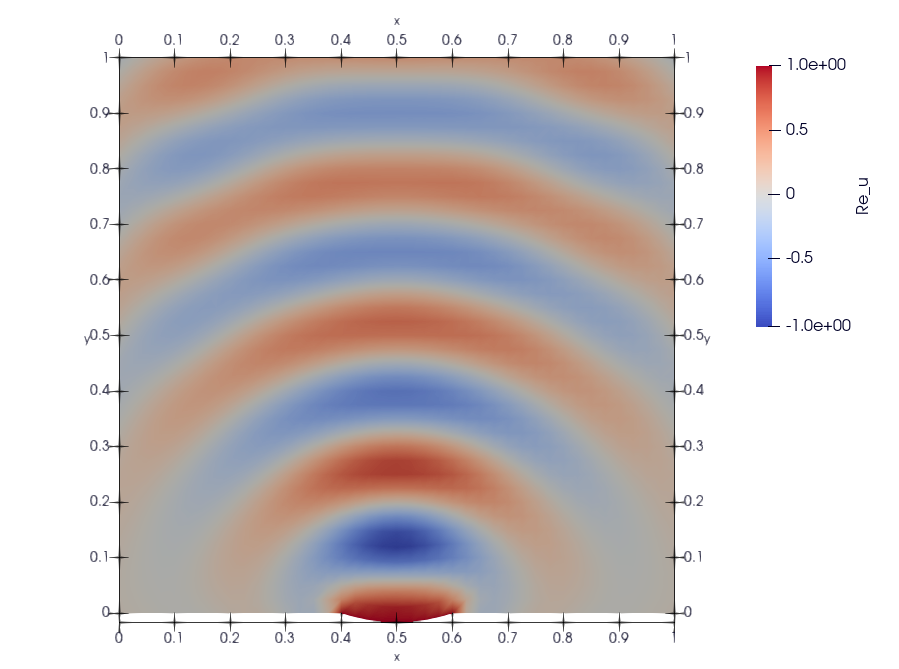
Сл. 44 Решење за \(v=\textrm{Re} \; u\) добијено методом коначних елемената
Квалитативно гледано, НМПФЗ решење има исте карактеристике као МКЕ решење. Међутим, око сочива и прима границама \(\Gamma_2\) очигледан је пад квалитета решења. Узрок можемо тражити на неколико места:
Прво, код МКЕ је извор на линији сочива \(\Gamma_1\) могуће прецизније специфицирати по самој линији, а не у појединачним тачкама као код НМПФЗ.
Могуће је да 50.000 колокационих тачака није довољно за обучавање.
Примећено је да обучавање оптимизационим алгоритам
Adamне може да спусти вредност губитка испод неке границе. Овде вероватно треба експериментисати са варијабилном стопом учења, или додати неки други оптимизатор као у примеру Пропагација таласа у отвореном каналу.
Даље експериментисање на овом примеру остављамо читаоцу.