Пример прорачуна производње
Аналитички модел
У овом одељку ћемо употребити методологију приказану у Увод и једноставни модел PVWatts објашњен у Основне једначине модела употребити на једном реалном примеру. У питању је соларна електрана у Централној Србији са 146 инсталисаних панела на крову једне зграде. Све карактеристике инсталације су нам познате (угао нагиба, азимут, врста панела, карактеристике инвертора и слично). Од података имамо и серије температуре ваздуха и компоненти осунчаности, тако да лако можемо аналитички, по једначинама (35), (36) и (37) да израчунамо производњу. У случају да поседујемо временску прогнозу, можемо приближно и да предвидимо будућу производњу користећи стандардни PVWatts модел.
Иако математика није компликована, за програмску имплементацију овог аналитичког модела користићемо помоћ библиотеке PVLIB Holmgren et al. [HHM18]. На наредном листингу приказан је део кода који се тиче учитавања, припреме података и извођења PVWatts модела.
1import numpy as np
2import pandas as pd
3import pvlib
4from pvlib.location import Location
5
6# Ucitaj podatke o vremenu i proizvodnji
7solcast_data = pd.read_csv("data_21.08.16_22.10.14.csv", index_col="Time")
8solcast_data.index = pd.to_datetime(solcast_data.index, dayfirst=True)
9
10# Nagib, azimut i lokacija panela
11surface_tilt = 7
12surface_azimuth = 290
13location = Location(latitude=43.905410, longitude=20.341986, altitude=243, tz="Europe/Belgrade", name="Pons Cacak")
14
15# Pomeri vreme za pola sata, izracunaj poziciju sunca u svakom trenutku
16times = solcast_data.index - pd.Timedelta('30min')
17solar_position = location.get_solarposition(times)
18solar_position.index += pd.Timedelta('30min')
19
20# Novi dataframe sa vrednostima za vrednosti osuncanosti DNI, GHI, DHI
21df_poa = pvlib.irradiance.get_total_irradiance(
22 surface_tilt=surface_tilt,
23 surface_azimuth=surface_azimuth,
24 dni=solcast_data['DNI'],
25 ghi=solcast_data['GHI'],
26 dhi=solcast_data['DHI'],
27 solar_zenith=solar_position['apparent_zenith'],
28 solar_azimuth=solar_position['azimuth'],
29 model='isotropic')
30
31# Izvuci ukupnu POA vrednost iz df_poa
32E_data = df_poa["poa_global"]
33# Izvuci temperaturu vazduha
34T_data = solcast_data["Tamb"]
35# Izvuci proizvodnju P
36P_data = solcast_data["P"]
37
38# Nedelju dana za treniranje
39E_data_train = E_data.loc["2021-10-31":"2021-11-06"]
40T_data_train = T_data.loc["2021-10-31":"2021-11-06"]
41P_data_train = P_data.loc["2021-10-31":"2021-11-06"]
42
43# Sledecih nedelju dana za testiranje
44E_data_test = E_data.loc["2021-11-07":"2021-11-13"]
45T_data_test = T_data.loc["2021-11-07":"2021-11-13"]
46P_data_test = P_data.loc["2021-11-07":"2021-11-13"]
47
48#
49# Parametri modela
50#
51pdc0 = 0.375 # nominal power [kWh]
52Tref = 25.0 # cell reference temperature
53gamma_pdc = -0.005 # influence of the cell temperature on PV system
54pdc0_inv = 50
55eta_inv_nom = 0.96
56eta_inv_ref = 0.9637
57pac0_inv = eta_inv_nom * pdc0_inv # maximum inverter capacity
58a = -2.98 # cell temperature parameter
59b = -0.0471 # Wind coefficient
60E0 = 1000 # reference irradiance
61deltaT = 1 # cell temperature parameter
62num_of_panels = 146 # Broj panela u instalaciji
63
64#
65# Originalni PVWAtts model
66#
67def orig_pvwatts_model(x):
68 Ta = x[:,0:1] # Temperatura vazduha
69 E = x[:,1:2] # Ukupna POA osuncanost
70
71 Tm = E * np.exp(a+b*2) + Ta # Brzina vetra uzeta kao prosecna od 2 m/s
72 Tc = Tm + E/E0*deltaT
73 P_dc_temp = ((Tc-Tref) * gamma_pdc + 1.)
74 P_dc = (E * 1.e-03 * pdc0 * P_dc_temp) * num_of_panels
75 zeta = (P_dc+1.e-2)/pdc0_inv
76
77 eta = eta_inv_nom/eta_inv_ref * (-0.0162*zeta - 0.0059/zeta + 0.9858)
78 eta[eta<0] = 0.
79 ac = np.minimum(eta*P_dc, pac0_inv)
80
81 return ac
Након стандардних импорта библиотека, учитавамо сатне серије података о времену:
Ta- температура ваздуха,DNI,GHI,DHI- компоненте осунчаности
и податке о производњи P у Pandas оквир. На жалост, немамо доступне податке о брзини ветра на локацији, па ћемо ту компоненту узети као просечну на том поднебљу, тј. вредност од \(2\,m/s\). Функција pvlib.irradiance.get_total_irradiance() библиотеке PVLIB нам израчунава положај сунца за било који временски тренутак и било коју локацију на Земљи, а на основу њега и укупну осунчаност панела чији је положај дат угловима surface_tilt и surface_azimuth. Као улаз, ова метода узима компоненте DNI, GHI и DHI дефинисане у одељку Компоненте зрачења.
Након екстракције периода од недељу дана од 31. октобра до 6. новембра и другог периода од 7. до 13. новембра, постављамо све параметре који се користе у једначинама (35), (36) и (37), онако како најбоље одговара самој инсталацији. Сви параметри осим три су константе прихваћене у литератури. Та три параметра чија вредност може да се подешава су a и b из израза (35) и gamma_pdc из израза (36). Њихове вредности (-2,98, -0.0471 и -0,005 респективно) задајемо према врсти панела и начину постављања инсталације.
Поређење резултата добијених чистим моделом и мерених вредности може се видети на Сл. 61. Очигледно је да постоји значајно одступање, тј. модел даје више вредности од мерења. Корен средње квадратне грешке (RMSE) износи чак 2,46 kW. Одређени допринос овако високој вредности грешке сигурно је последица чињенице да хлађење панела услед утицаја ветра нисмо узели у обзир услед недостатка података о ветру.
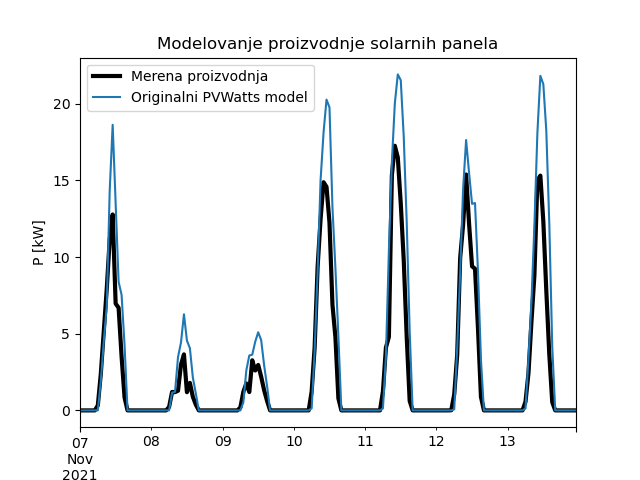
Сл. 61 Поређење чистог PVWAtts модела са мереном производњом
Ниједан модел није савршена слика стварности и не може да обухвати све факторе који утичу на производњу. Чак иако је модел савршен (а не може бити), могуће су појаве грешака при мерењу температуре, осунчаности, брзине ветра. Даље, код самог модела имамо више параметара чије вредности узимамо из литературе и декларације произвођача. Реалне вредности тих параметара сигурно одступају од тих вредности и мењају се током животног века уређаја.
Подешавање параметра помоћу НМПФЗ
Поставља се питање да ли вредности које даје модел могу бити приближније реалним вредностима само подешавањем параметара модела. Пробаћемо да искористимо чињеницу да податке о производњи за недељу од 31. октобра имамо и да помоћу НМПФЗ пробамо да „помиримо” излаз аналитичког модела и мерења производње тако што ћемо параметар a једначине (36) прогласити непознатим. Основна идеја је да се НМПФЗ тренира и једначином и подацима и да као излаз испоручи и модел са мањом грешком и нову, бољу вредност параметра a.
На следећем листингу могу се видети интересантни делови имплементације ове идеје:
1# Parametar "a" pustamo da se trenira
2a_var = dde.Variable(-4.0)
3
4#
5# Jednacina koju koristi PINN
6#
7def pvwatts_eq(x, y):
8 Ta = x[:,0:1] # Temperatura vazduha
9 E = x[:,1:2] # Ukupna POA osuncanost
10
11 Tm = E * tf.exp(a_var+b*2) + Ta # Brzina vetra uzeta kao prosecna od 2 m/s
12 Tc = Tm + E/E0*deltaT
13 P_dc_temp = ((Tc-Tref) * gamma_pdc + 1)
14 P_dc = (E * 1.e-03 * pdc0 * P_dc_temp) * num_of_panels
15 zeta = (P_dc+1.e-2)/pdc0_inv
16
17 eta = eta_inv_nom/eta_inv_ref * (-0.0162*zeta - 0.0059/zeta + 0.9858)
18 eta = tf.maximum(0., tf.sign(eta)) * eta
19 ac = tf.minimum(eta*P_dc, pac0_inv)
20
21 return y - ac
22
23# Imamo 168 tacaka sa merenjima proizvodnje. Pripremi strukturu za PointSet granicni uslov
24train_points = np.zeros((168,2))
25train_measured_production = np.zeros((168,1))
26train_points[:,0] = T_data_train.to_numpy().T
27train_points[:,1] = E_data_train.to_numpy().T
28train_measured_production[:,0] = P_data_train.to_numpy().T
29
30# Imamo 168 tacaka sa merenjima za narednu nedelju za test
31test_points = np.zeros((168,2))
32test_measured_production = np.zeros((168,1))
33test_points[:,0] = T_data_test.to_numpy().T
34test_points[:,1] = E_data_test.to_numpy().T
35test_measured_production[:,0] = P_data_test.to_numpy().T
36
37# Minimumi i maksimumi T i E za kreiranje geometrije problema
38minT, maxT = min(train_points[:,0]), max(train_points[:,0])
39minE, maxE = min(train_points[:,1]), max(train_points[:,1])
40
41geom = dde.geometry.Rectangle([minT, minE], [maxT, maxE])
42bc_y = dde.icbc.PointSetBC(train_points, train_measured_production, component=0)
43
44# Isti broj kolokacionih tacaka za jednacinu i za granicne uslove. Moze i drugacije.
45data = dde.data.PDE(geom, pvwatts_eq, [bc_y], 168, 168, solution = orig_pvwatts_model, num_test=100)
46
47layer_size = [2] + [30] * 5 + [1]
48activation = "tanh"
49initializer = "Glorot uniform"
50net = dde.nn.FNN(layer_size, activation, initializer)
51
52variable_a = dde.callbacks.VariableValue(a_var, period=1000)
53model = dde.Model(data, net)
54
55model.compile(optimizer="adam", lr=0.001, metrics=["l2 relative error"], external_trainable_variables=[a_var])
56losshistory, train_state = model.train(iterations=20000, callbacks=[variable_a])
57predicted_test = model.predict(test_points)
58
59# Predikcije manje od nule nemaju smisla. Nuluj ih.
60predicted_test[predicted_test<0]=0
Као и код раније обрађених инверзних проблема који користе библиотеку DeepXDE, постављамо параметар као варијаблу чија се вредност добија процесом обучавања:
a_var = dde.Variable(-4.0)
Ако погледамо функцију pvwatts_eq(x, y), она је готово идентична функцији orig_pvwatts_model(x) са Листинг 12. Разлика је у томе што pvwatts_eq(x, y) не враћа вредност снаге, већ функцију губитка, као што смо већ навикли. Још једна разлика огледа се у коришћењу TensorFlow логике уместо условног израза:
eta = tf.maximum(0., tf.sign(eta)) * eta
Овај израз није ништа друго него услов да ако имамо нефизичку вредност eta<0 поставимо да је eta=0. Овом формулацијом избегавамо инструкцију условног скока, која се на графичком процесору изводи доста спорије од чистог рачуна у покретном зарезу.
У даљем току програма треба да поставимо структуру за посебан гранични услов PointSet, који смо већ користили у одељку Инверзни проблем и Пропагација таласа у отвореном каналу:
train_points = np.zeros((168,2))
train_measured_production = np.zeros((168,1))
train_points[:,0] = T_data_train.to_numpy().T
train_points[:,1] = E_data_train.to_numpy().T
train_measured_production[:,0] = P_data_train.to_numpy().T
bc_y = dde.icbc.PointSetBC(train_points, train_measured_production, component=0)
Имамо укупно 168 тачака (7x24) мерења производње које ћемо искористити у покушају да „спустимо” вредности које даје оригинални модел. Геометрију проблема који решавамо дефинишемо опсегом улазних варијабли температуре и укупне осунчаности, које се узимају из табеле података. Онда можемо да поставимо и колокационе тачке на домену наредбом:
data = dde.data.PDE(geom, pvwatts_eq, [bc_y], 168, 168, solution = orig_pvwatts_model, num_test=100)
За број случајних колокационих тачака унутар домена узели смо исти број тачака колико имамо у PointSet граничном услову. Није нужно да број тачака буде једнак, па остављамо читаоцу да експериментише различитим вредностима. Остатак кода је мање-више исти као код свих других примера који користе DeepXDE за решавање инверзних проблема. Ту је постављање архитектуре НМПФЗ и хипер-параметара, алгоритма оптимизације, стопе обуке, callback функције за штампу тренутне вредности a_var током обуке и слично. На крају се анулирају негативне вредности предвиђене производње јер немају физичког смисла.