Пример конструкције функције губитка

Резоновање из претходног одељка Неуронске мреже подржане физичким законима ћемо поткрепити једноставним примером. Започнимо прво тако што ћемо узети неку једноставну диференцијалну једначину. Изабраћемо логистичку једначину (Logistic Equation) која представља модел раста популације. Та једначина гласи:

(4)\[\frac{df}{dt} = R \cdot t(1-t)\]

Функција \(f(t)\) представља стопу раста популације током времена \(t\), док параметар \(R\) одређује максималну стопу раста. Како бисмо од фамилије кривих које задовољавају решење ове обичне диференцијалне једначине изабрали једну криву као решење, морамо поставити гранични, тј. почетни услов. Нека то буде:

(5)\[f(t=0) = \frac{1}{2}.\]

Како је аналитичко решење ове једначине познато, поређењем са њим можемо проверити тачност НМПФЗ. Тиме ћемо почети да разоткривамо потенцијал примене и на комплексније обичне и парцијалне диференцијалне једначине. Да се подсетимо, НМПФЗ су засноване на две фундаменталне особине неуронских мрежа:

• Формално је показано да су неуронске мреже универзалне функције апроксимације, тако да неуронска мрежа може да апроксимира било коју функцију, а самим тим и решење за нашу логистичку једначину.

• Једноставно је и јефтино израчунати изводе било ког реда излаза из неуронске мреже за било који дати улаз коришћењем аутоматске диференцијације.

Дакле, као што је речено, можемо да конструишемо функцију губитка тако да, када се минимизује, диференцијална једначине буде задовољена:

(6)\[\mathcal{L}_{r} = \frac{df_{NN}(t)}{dt} - R \cdot t(1-t) = 0,\]

где је \(f_{NN}(t)\) излаз неуронске мреже са једним улазом чији се извод израчунава аутоматским диференцирањем. Одмах видимо да, уколико излаз из мреже задовољава (6), заправо се та једначина решава. Да би се израчунао стварни допринос функцији губитка који се добија из диференцијалне једначине, потребно је специфицирати скуп тзв. колокационих тачака у домену проблема и проценити средњу квадратну грешку (Mean Squared Error - MSE) или неку другу функцију губитка:

(7)\[\mathcal{L}_{r} = \frac{1}{N_{r}}\sum_{i = 1}^{N_{r}} \left( \left. \frac{df_{NN}}{dt} \right|_{t_i} - R t_j (1-t_i) \right)^2,\]

где je \(N_{r}\) број колокационих тачака \(t_j\) у којима се рачуна функција губитка. Губитак заснован само на резидуалима не осигурава јединствено решење, па стога укључујемо и гранични услов, тако што га додајемо функцији губитка на исти начин као у једначини (7):

(8)\[\mathcal{L}_{0} = \frac{1}{N_{0}}\sum_{i = 1}^{N_{0}} \left( \left. f_{NN}(t) \right|_{t_i} - \frac12 \right)^2, \qquad t_i \approx 0.\]

Сада имамо оба елемента да дефинишемо укупну функцију губитка \(\mathcal{L}\):

(9)\[\mathcal{L} = \mathcal{L}_{r} + \mathcal{L}_{0}.\]

Током тренирања неуронске мреже, горњи израз се минимизује и излаз из мреже тренира да задовољи диференцијалну једначину и задат гранични услов, чиме се апроксимира коначно, јединствено решење диференцијалне једначине. Концепт НМПФЗ је веома једноставан, и користећи идеју описану у претходном тексту, можемо додати више граничних услова, додати комплексније или решавати временски зависне вишедимензионалне проблеме користећи мрежу са вишеструким улазима.

Решење наше логистичке једначине је добро позната сигмоидна функција приказана на Сл. 2.

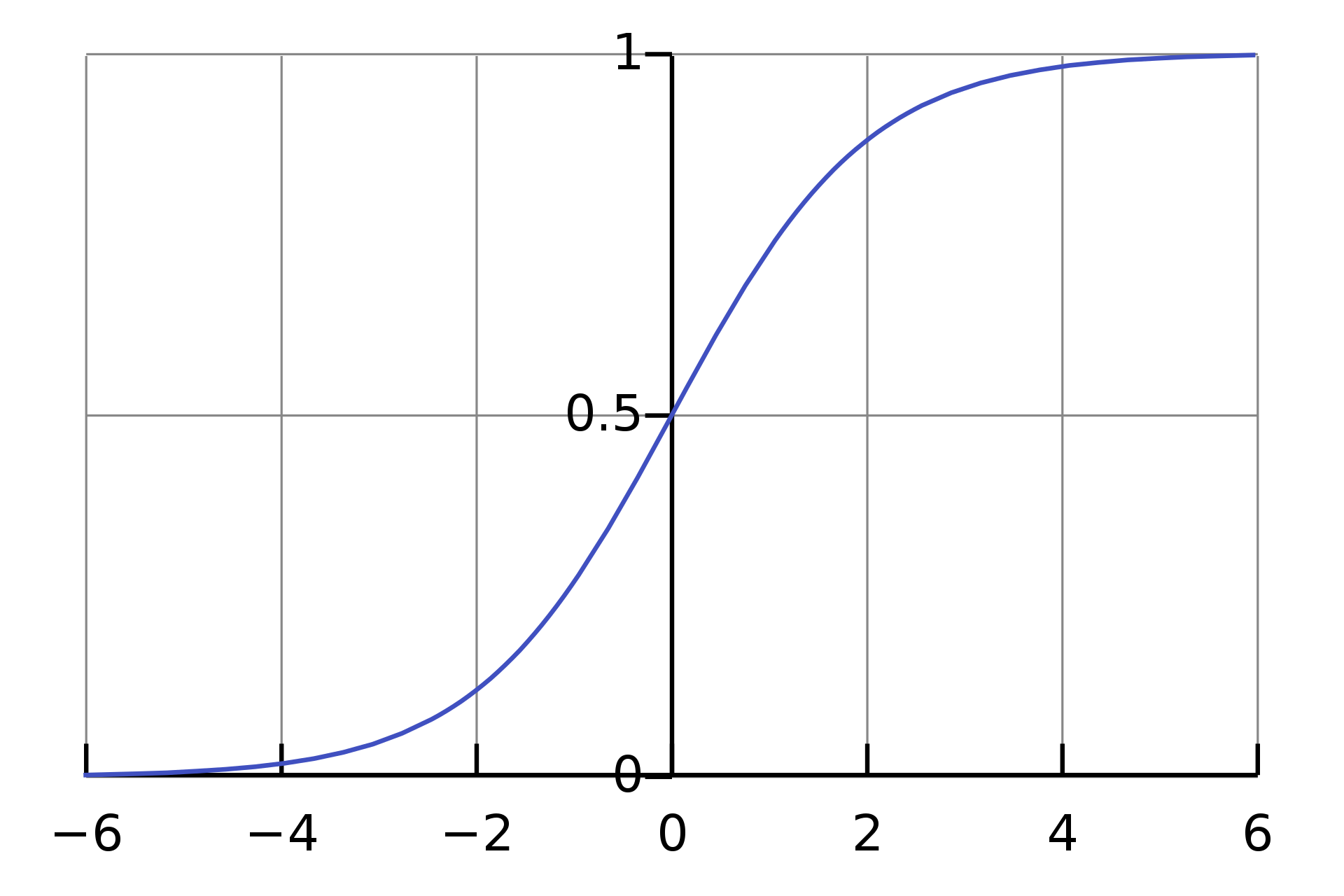
Сл. 2 Сигмоидна функција која се добија као решење једначине (4) са почетним условом (5)

Начин излагања примера

Излагање ћемо наставити конкретним примерима. Свако поглавље практикума (Провођење топлоте, Осцилације, …) бави се посебном феноменологијом и садржи по један или више директних или инверзних решених проблема. Сваки пример је поткрепљен теоријском позадином, припадајућим програмским кодом који имплементира НМПФЗ решење, као и анализом тачности и ефикасности НМПФЗ решења у односу на аналитичка решења, уколико постоје, или решења добијена класичним нумеричким методама.

Ваља напоменути да примери нису сортирани по тежини, већ искључиво по феноменологији која се моделује. Ако ипак треба да препоручимо читаоцу одакле да крене са практичним радом, рецимо да Механичке осцилације и Једнодимензиони директни проблем представљају добру основу.