Једнодимензиони директни проблем

Танак штап од хомогеног материјала је окружен изолацијом, тако да се промене температуре у штапу дешавају само као последица размене топлоте ка крајевима штапа и провођења топлоте дуж штапа. Штап је јединичне дужине. Оба краја су изложена мешавини воде и леда температуре 0. Почетна температура на растојању \(x\) од левог краја штапа је \(sin{(\pi x)}\), као што се види на Сл. 3.

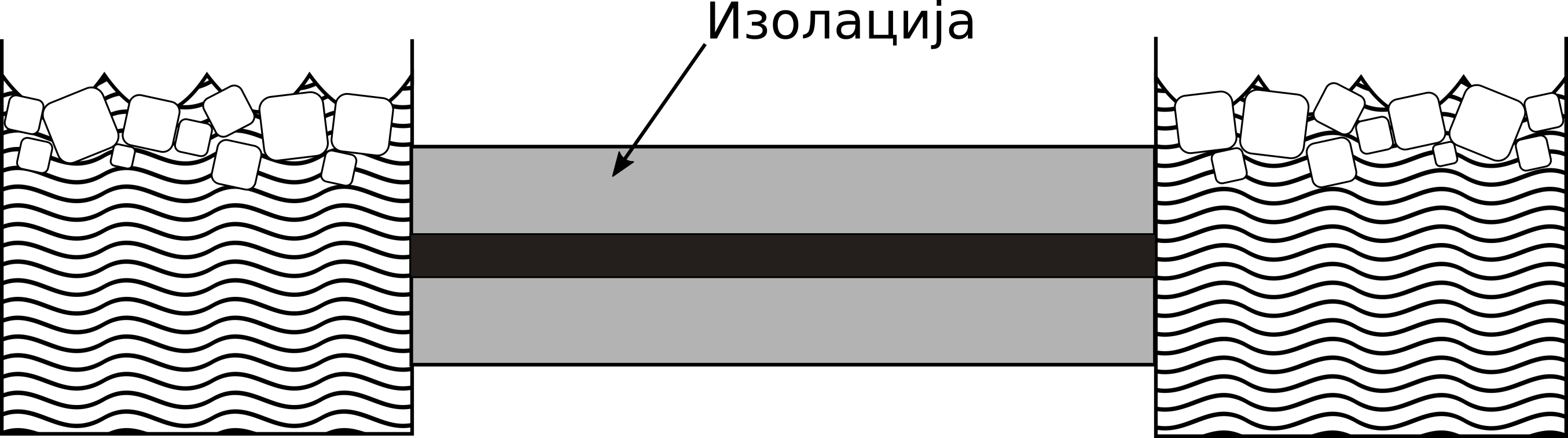
../_images/fdheat.png

Сл. 3 Експериментална поставка проблема провођења топлоте дуж штапа. На крајевима штапа налази се мешавина воде и леда. Штап је изолован од утицаја спољашње средине.

Ради поређења, показаћемо сада како се овај релативно једноставан проблем формулише помоћу класичне методе коначних разлика, а затим ћемо решити директни и инверзни проблем описане поставке НМПФЗ методом.

Решавање методом коначних разлика (МКР)

Парцијална диференцијална једначина (10) моделује температуру у било којој тачки штапа у било ком временском тренутку према Recktenwald [Rec04]. Ова једначина се решава методом коначних разлика, која даје апроксимацију решења за распоред температуре, примењујући просторну и временску дискретизацију. Програмска имплементација решења чува температуру сваке тачке дискретизације у дводимензионој матрици. Сваки ред садржи температурну дистрибуцију штапа у неком тренутку времена. Штап је подељен на \(n\) делова дужине \(h\), па стога сваки ред има \(n+1\) елемената. Начелно, што је веће \(n\), мања је грешка апроксимације. Време од 0 до \(T\) је подељено у \(m\) дискретних интервала дужине \(k\), па стога матрица има \(m+1\) редова, као што је приказано на Сл. 5.

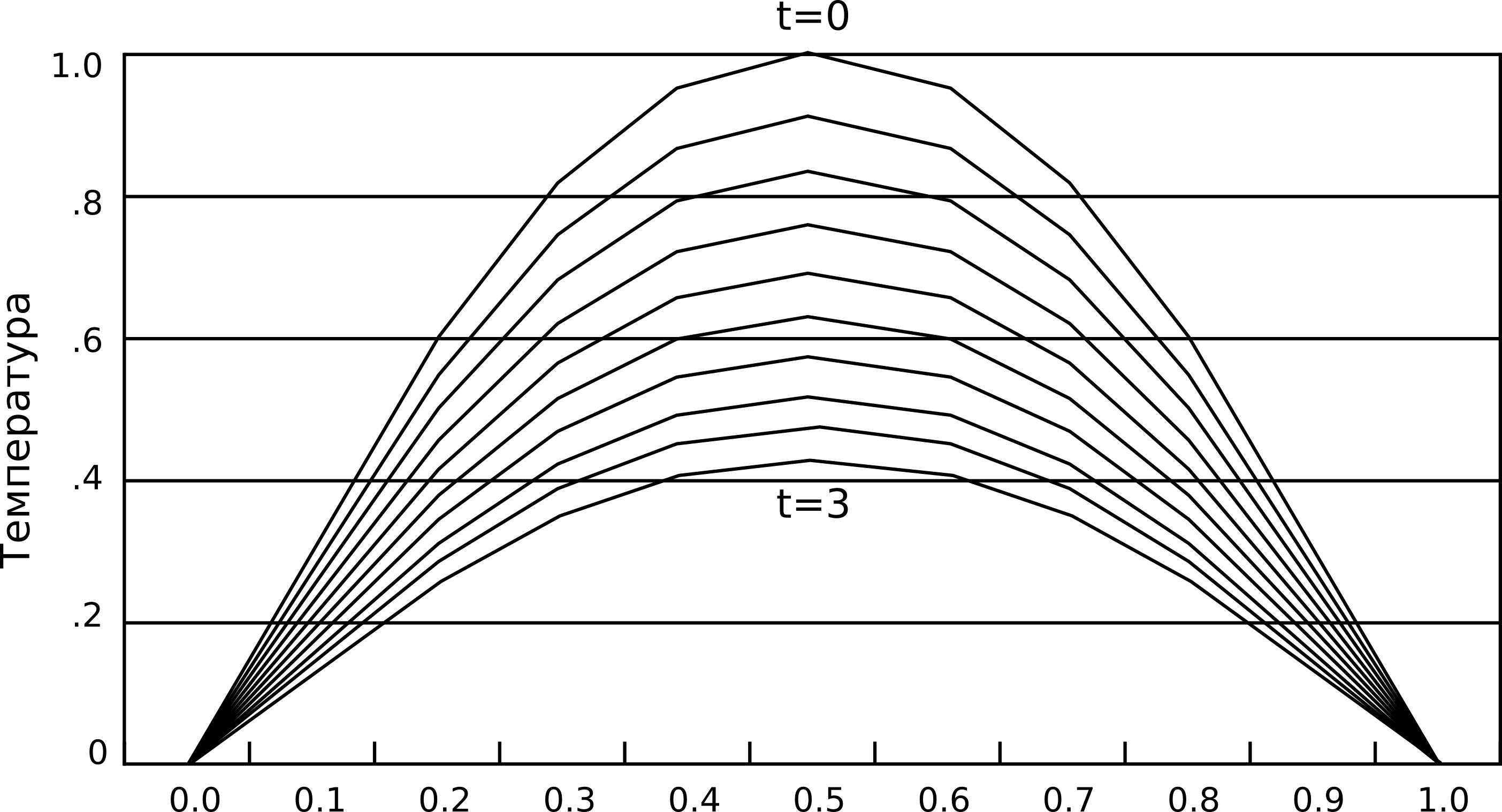
../_images/fdheat1.png

Сл. 4 Како време тече, штап се хлади. Метода коначних разлика омогућава израчунавање температуре у фиксном броју тачака у равномерним временским интервалима. Смањење просторног и временског корака углавном доводи до прецизнијег решења.

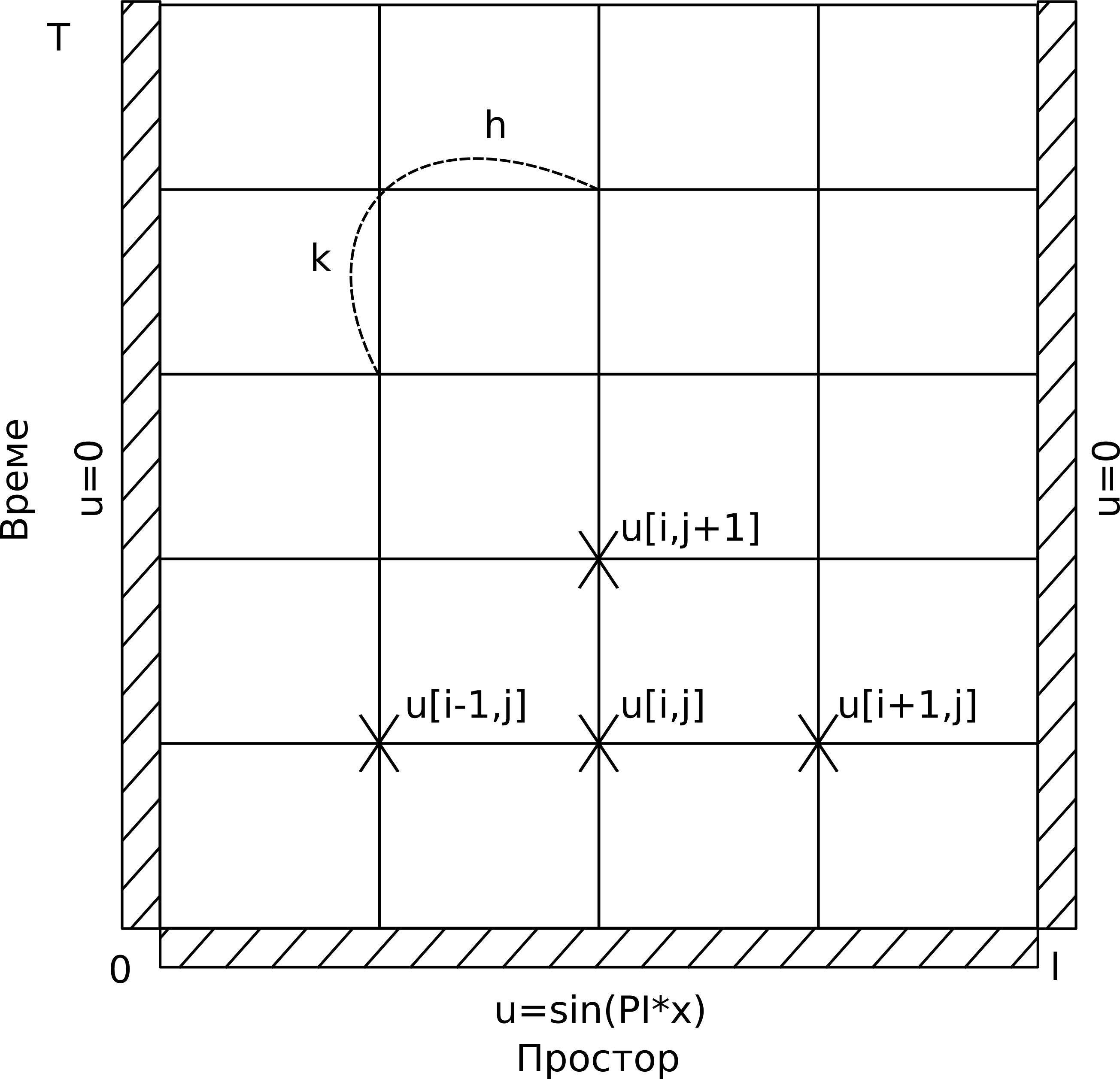
../_images/fdheat2.png

Сл. 5 Дискретизација једначине провођења топлоте методом коначних разлика

Свака тачка \(u_{i,j}\) представља елемент матрице који садржи температуру на позицији \(i \cdot h\), у тренутку \(j \cdot k\). На крајевима штапа је температура увек нула. У почетном тренутку, температура у тачки \(x\) је, као што је већ речено, \(sin{(\pi x)}\). Алгоритам иде корак по корак кроз време, користи вредности из тренутка \(j\) да би израчунао вредности у тренутку \(j+1\). Формула која репрезентује варијанту апроксимације FTCS (Forward Time Centered Space) као у Recktenwald [Rec04] се овде даје без извођења и гласи:

(11)\[u_{i,j+1} = R \cdot u_{i-1,j}+(1-2R) \cdot u_{i,j} + R \cdot u_{i+1,j},\]

где је

\[R = \alpha \frac{k}{h^2}.\]

Целокупна анализа различитих експлицитних и имплицитних метода дата је у поменутој референци, а кључни део кода у програмском језику Пајтон имплементиран је на следећи начин:

 1 def heatFTCS(nt=10, nx=20, alpha=0.3, L=1, tmax=0.1):
 2     h = L / (nx - 1)
 3     k = tmax / (nt - 1)
 4     r = alpha * k / h**2
 5
 6     x = np.linspace(0, L, nx)
 7     t = np.linspace(0, tmax, nt)
 8     U = np.zeros((nx, nt))
 9
10     # Почетни услов
11     U[:, 0] = np.sin(np.pi * x / L)
12
13     # Главна петља за МКР
14     for m in range(1, nt):
15         for i in range(1, nx-1):
16             U[i, m] = r * U[i - 1, m - 1] + (1-2*r) * U[i, m-1] + r * U[i+1, m-1]
17
18     # Егзактно решење за поређење
19     ue = np.sin(np.pi * x / L) * \
20         np.exp(-t[nt - 1] * alpha * (np.pi / L) * (np.pi / L))

Као што детаљно објашњава Recktenwald [Rec04], ако се МКР петља формулише експлицитно као што је то случај код FTCS технике, мора се пажљиво изабрати временски и просторни корак, како би нумеричка пропагација била „бржа” од физичке. Решење које се добија помоћу МКР шеме се може видети на Сл. 6.

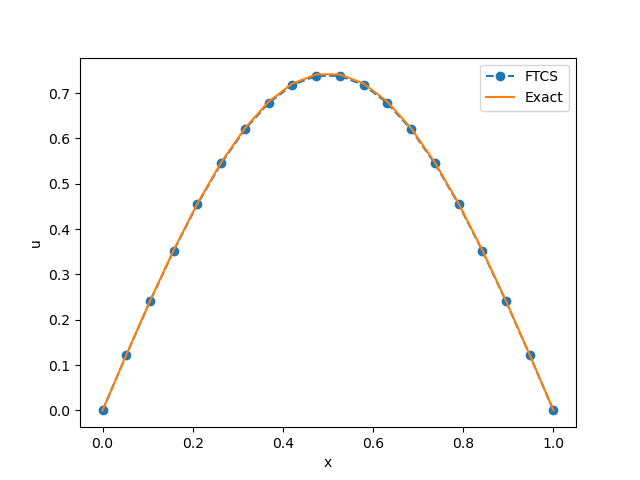
../_images/ftcs.png

Сл. 6 Решење које се добија МКР методом користећи експлицитну FTCS технику у тренутку \(t=0.1s\)

Овај проблем има и аналитичко решење, па је погодан за тестирање различитих нумеричких метода. То решење гласи:

(12)\[u(x,t) = \sin\left(\frac{\pi x}{L}\right) \cdot e^{-\frac{\alpha\pi^2}{L^2}t}.\]

или у нашем случају, када је \(L=1\):

\[u(x,t) = \sin(\pi x) \cdot e^{-\alpha \pi^2 t}.\]

Експлицитне технике попут FTCS не гарантују конзистентност решења коју гарантују имплицитне технике као што је BTCS (Backward Time Centered Space). МКР је устаљени приступ који за већину правилно дефинисаних просторних домена ради веома добро. За овако једноставну поставку као што је једнодимензионо провођење топлоте и када су сви параметри проблема познати (овде је то \(\alpha\)), МКР је често оптимална метода. Међутим, код већине проблема из праксе то није случај. Хајде да размотримо како да овај проблем решимо користећи НМПФЗ и директно упоредимо са МКР.

Решавање помоћу НМПФЗ

Решење једначине Сл. 3 са већ постављеним граничним и почетним условима:

(13)\[\begin{split}u(x=0,t)=u(x=1,t)=0, \, \forall t \\ u(x,t=0) = sin{(\pi x)}\end{split}\]

потражићемо помоћу НМПФЗ приступа. Иако је могуће да методе имплементирамо директно као Raissi et al. [RPK19] користећи оквир за дубоко учење као што је Tensorflow, ипак ћемо искористити помоћ библиотека које додатно апстрахују НМПФЗ ентитете и омогућавају кориснику да се фокусира на проблем који решава. Овај пример решићемо користећи библиотеку SCIANN аутора Haghighat and Juanes [HJ21]. Поступак решавања објаснићемо директно кроз програмски код:

Листинг 1 НМПФЗ - провођење топлоте
 1 import numpy as np
 2 import sciann as sn
 3 from sciann.utils.math import diff, sign, sin, sqrt, exp
 4 from numpy import pi
 5
 6 x = sn.Variable('x')
 7 t = sn.Variable('t')
 8 u = sn.Functional('u', [x,t], 3*[20], 'tanh')
 9 alpha = 0.3
10
11 L1 = diff(u, t) - alpha * diff(u, x, order=2)
12
13 TOLX = 0.011
14 TOLT = 0.0011
15 C1 = (1-sign(t - TOLT)) * (u - sin(pi*x))
16 C2 = (1-sign(x - (0+TOLX))) * (u)
17 C3 = (1+sign(x - (1-TOLX))) * (u)
18
19 m = sn.SciModel([x, t], [L1, C1, C2, C3], 'mse', 'Adam')
20
21 x_data, t_data = np.meshgrid(
22     np.linspace(0, 1, 101),
23     np.linspace(0, 0.1, 101)
24 )
25
26 h = m.train([x_data, t_data], 4*['zero'], learning_rate=0.002, batch_size=256, epochs=500)
27
28 # Test
29 nx, nt = 20, 10
30 x_test, t_test = np.meshgrid(
31     np.linspace(0.01, 0.99, nx+1),
32     np.linspace(0.01, 0.1, nt+1)
33 )
34 u_pred = u.eval(m, [x_test, t_test])

Варијабле \(x\) и \(t\) се на почетку дефинишу на прописани начин. Основни појам који се користи у SCIANN библиотеци за апстракцију НМПФЗ је функционал, који је овде означен са \(u\), који као улаз узима \(x\) и \(t\), има 3 скривена слоја са по 20 неурона и као активацију свих тих неурона узима функцију хиперболичког тангенса. Први сабирак композитне функције губитка произилази из саме диференцијалне једначине (10). Као што се види, за диференцирање се користи специјални оператор diff() из библиотеке:

L1 = diff(u, t) - alpha * diff(u, x, order=2)

Најзанимљивији и не баш тако очигледан је начин дефинисања почетног услова C1 и граничних услова C2 и C3:

C1 = (1-sign(t - TOLT)) * (u - sin(pi*x))
C2 = (1-sign(x - (0+TOLX))) * (u)
C3 = (1+sign(x - (1-TOLX))) * (u)

Овде је C1 једнак нули у свим тачкама узорковања осим за \(t \le TOLT\). Толеранције TOLX и TOLT су постављене тако да „хватају” прву/последњу врсту или колону колокационих тачака, у зависности шта је потребно. Уместо функције знака sign(), могу се користити и глаткије функције, као што је хиперболички тангенс. НМПФЗ модел се формира помоћу SciModel конструктора који дефинише и тип функције губитка и алгоритам оптимизације, тј. обучавања:

m = sn.SciModel([x, t], [L1, C1, C2, C3], 'mse', 'Adam')

Обучавање модела се покреће методом train(), при чему се наводе следећи параметри:

  1. Скуп колокационих тачака за тренирање. Овде је то правилна еквидистантна мрежа тачака по обе варијабле. Хоризонтала је простор, а вертикала време.

  2. Почетне вредности компоненти функције губитка. Уобичајено је да се на почетку поставе на нуле.

  3. Стопа учења,

  4. Величина batch-a. Треба имати на уму да ако је број тачака домена у којима се намећу гранични услови значајно мањи у односу на укупан број колокационих тачака, параметар оптимизације batch_size треба да буде подешен на велики број који гарантује доследну оптимизацију мини batch-a. У супротном, може да се деси да неки мини batch-еви не добију ниједну колокациону тачку која припада граничним условима и стога не генеришу тачан градијент за ажурирање методом градијентног спуста.

  5. Број епоха.

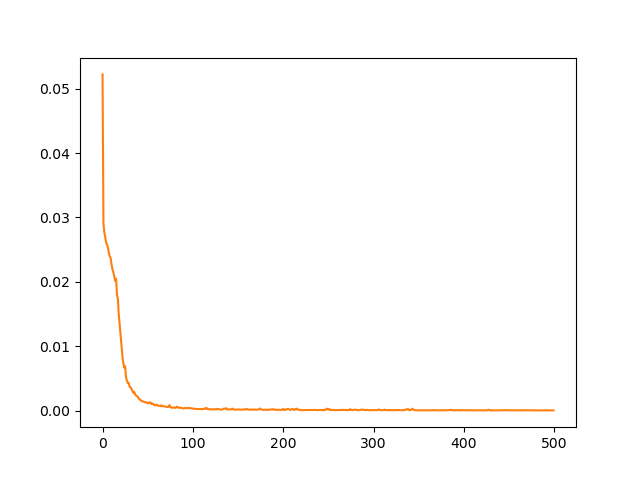
../_images/loss1.png

Сл. 7 Историја обуке једнодимензионог модела провођења топлоте.

Ток обуке можемо да испратимо кроз стандардне Tensorflow објекте, као што је h.history['loss'], као што се види на Сл. 7. Пошто се заврши обука НМПФЗ-а, можемо формирати тестни скуп тачака слично као што смо то учинили и са колокационим тачкама и проверити резултате предикције позивом методе eval() на објекту истренираног модела. Резултат поља температуре дуж штапа у тренутку \(t=0,1\) и његово поређење са аналитичким решењем види се на Сл. 8.

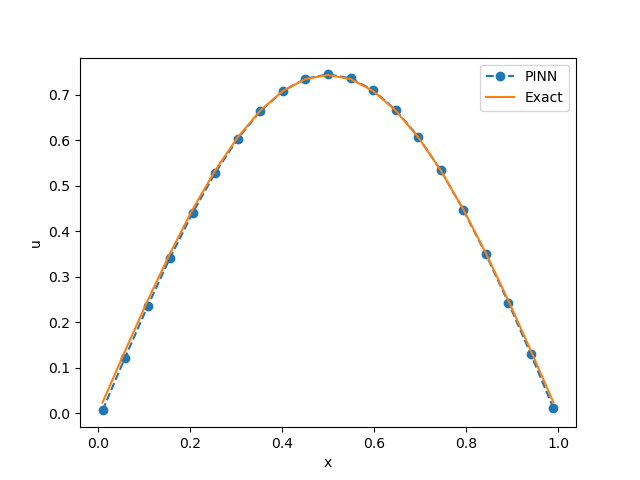
../_images/heat-pinn1.png

Сл. 8 Поље температуре дуж штапа у тренутку \(t=0,1\) добијено методом НМПФЗ.

Чисто практично гледано, НМПФЗ решење једноставног директног проблема као што је овај и не пружа никакве посебне предности у односу на класичну МКР методу. Прво, решавање дуже траје и захтева упошљавање више рачунарских ресурса и зависности у виду додатних библиотека за тензорски рачун. Даље, спецификација почетних и граничних услова код НМПФЗ има своје специфичности. Треће, неопходно је методом пробе и грешке подесити хипер-параметре модела, као што су: број скривених слојева, број неурона по слоју, активациона функција, брзина учења (Learning Rate) итд. Од избора хипер-параметара конвергенција решења може значајно да зависи.

Са друге стране, за разлику од МКР и МКЕ (Метода Коначних Елемената), НМПФЗ нам дозвољава да проблем дефинишемо чистим диференцијалним једначинама и произвољним граничним условима (Дирихлеови, Нојманови, периодични, скуп тачака). Нема потребе за специфицирањем алгебарске везе између чворова (тј. колокационих тачака у НМПФЗ) и решавањем тако постављеног система једначина. Захваљујући овој чињеници, било која нова физика у виду новог граничног услова или промена у самој диференцијалној једначини може да се изведе веома лако, омогућавајући брзу проверу хипотеза и израду прототипова.

Друго, док све класичне методе прорачун морају да изведу кроз временске кораке (time stepping), НМПФЗ омогућава брзу инференцију на већ обученој мрежи за било који временски тренутак \(t\) постављен на улазу мреже. За неке примене у реалном времену где је брзина од кључног значаја, ово може да буде пресудно.

Треће, НМПФЗ методолошки не разликује директне проблеме (у којима се решава позната диференцијална једначина) од инверзних проблема, код којих су неки од параметара непознати, али постоје додатни услови из којих се непознати параметри могу добити процесом тренинга. У наредној теми Једнодимензиони инверзни проблем демонстрираћемо један такав проблем.