Једнодимензиони инверзни проблем

Поставка инверзног проблема је потпуно иста као и у претходном поглављу Једнодимензиони директни проблем, тј. описана је Сл. 3, једначином (10) и граничним условима (13). Међутим, овога пута нам параметар проблема \(\alpha\) на почетку није познат и покушаћемо да га добијемо уз помоћ метода обучавања пропагацијом уназад. Наравно, чим смо увели нову непознату, морамо да уведемо и нови гранични услов. Рецимо, можемо да поставимо да је у једној тачки у неком временском тренутку, температура \(u\) одговарала некој нумеричкој вредности која се поклапа са аналитичким решењем (12). Рецимо, поставимо температуру на средини штапа у \(x=0,5\) у тренутку \(t=0,05\) на:

\[u(x=0,5, t=0,05) = 0,8623931,\]

и покушајмо да решимо проблем постављајући граничне услове на следећи начин:

Листинг 2 Проналажење непознатог параметра \(\alpha\)
 1x = sn.Variable('x')
 2t = sn.Variable('t')
 3u = sn.Functional('u', [x,t], 3*[20], 'tanh')
 4alpha = sn.Parameter(0.5, inputs=[x,t], name="alpha")
 5
 6L1 = diff(u, t) - alpha * diff(u, x, order=2)
 7
 8TOL = 0.011
 9TOLT= 0.0011
10C1 = (1-sign(t - TOLT)) * (u - sin(pi*x))
11C2 = (1-sign(x - (0+TOL))) * (u)
12C3 = (1+sign(x - (1-TOL))) * (u)
13C4 = (1 + sign(t-0.049)) * (1 - sign(t-0.051)) * (1 + sign(x-0.49)) * (1 - sign(x-0.51)) * (u-0.8623931)
14
15m = sn.SciModel([x, t], [L1, C1, C2, C3, C4], 'mse', 'Adam')
16
17x_data, t_data = np.meshgrid(
18    np.linspace(0, 1, 101),
19    np.linspace(0, 0.1, 101)
20)
21
22h = m.train([x_data, t_data], 5*['zero'], learning_rate=0.002, batch_size=512, epochs=1200,
23    adaptive_weights={'method':'NTK', 'freq':100})
24
25# Test
26nx, nt = 20, 10
27x_test, t_test = np.meshgrid(
28    np.linspace(0.01, 0.99, nx+1),
29    np.linspace(0.01, 0.1, nt+1)
30)
31u_pred = u.eval(m, [x_test, t_test])
32
33print(alpha.value)

Очигледно је да је код готово исти као претходни у коме се решава директни проблем, јер је и методологија за решавање директних и инверзних проблема код НМПФЗ идентична. Једина разлика је у поставци. Линија 4 поставља \(\alpha\) као непознати параметар и даје му почетну вредност. У линији 13 се поставља додатни гранични услов у тачки u(x=0.4,t=0.05), који ће постати још једна компонента композитне функције губитка која се формира у линији 15. Вредност непознатог параметра се штампа у последњој линији и у нашем тесту износи око 0,308, што је довољно блиско реалној вредности од 0,3. Потврда задовољавајућег решења инверзног проблема приказана је и графички на Сл. 9.

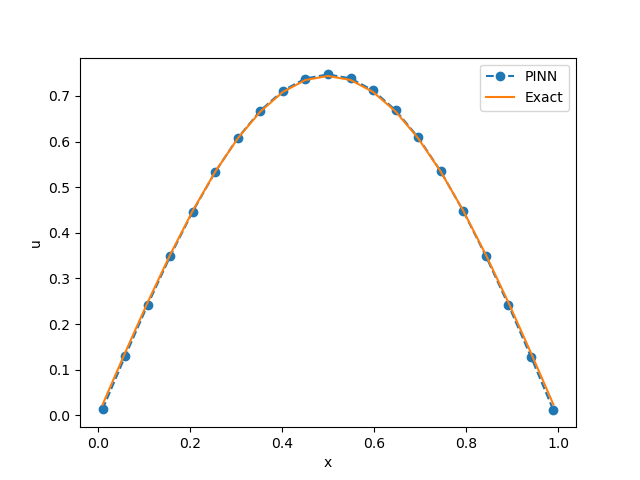
../_images/heat-inv.png

Сл. 9 Поље температуре дуж штапа у тренутку \(t=0,1\) добијено решавањем инверзног проблема