Стефанов проблем у моделима топљења

Након што смо успешно решили и директни и инверзни проблем провођења топлоте који је описан једноставном параболичном парцијалном диференцијалном једначином, позабавићемо се мало компликованијом поставком сличног проблема, пре свега имајући у виду граничне услове. Овде ће се они динамички мењати у зависности од градијента температуре. Показаћемо да је заправо овако постављен проблем лакше и природније решавати помоћу НМПФЗ-а него помоћу класичних нумеричких метода базираних на мрежи интеграционих тачака (МКЕ, МКР).

Стефанови проблеми фазних промена имају примену у разним областима науке и инжењерства, када год се фаза посматране супстанце мења између течног, чврстог или гасовитог стања. Претпоставља се да материјал пролази кроз фазну промену са кретањем границе, чији је положај непознат и мора се одредити као део саме нумеричке анализе. Пошто проблеми са померањем граница захтевају решавање топлотне једначине у непознатој области која се такође мора одредити као део решења, они су инхерентно нелинеарни.

Проблем једнодимензионалне промене фазе могао би се демонстрирати помоћу полубесконачног чврстог тела, као што је танак блок леда који заузима \(0 \le x < \infty\), на температури очвршћавања. На фиксној граници танког блока леда \(x=0\), могу да делују различите врсте флукса. У овом примеру користимо исти гранични услов као Ivanovic et al. [ISS17], Savovic and Caldwell [SC09], тако се температура при \(x=0\) повећава експоненцијално са временом. Такође, прописујемо да се читава чврста фаза налази на температури топљења. Стога сводимо проблем на одређивање расподела температуре у течној фази у време \(t_0\), где је \(x < s(t_0)\), као и положаја границе између фаза \(s(t_0)\).

У неком каснијем временском тренутку \(t_1 > t_0\), покретна граница \(s(t)\) креће се удесно, заузимајући позицију \(s(t_1) > s (t_0) = s_0\), као што је приказано на Сл. 10. Део танког блока леда од позиције \(s(t_0)\) до позиције \(s(t_1)\), отопио се током временског интервала \((t_0,t_1)\).

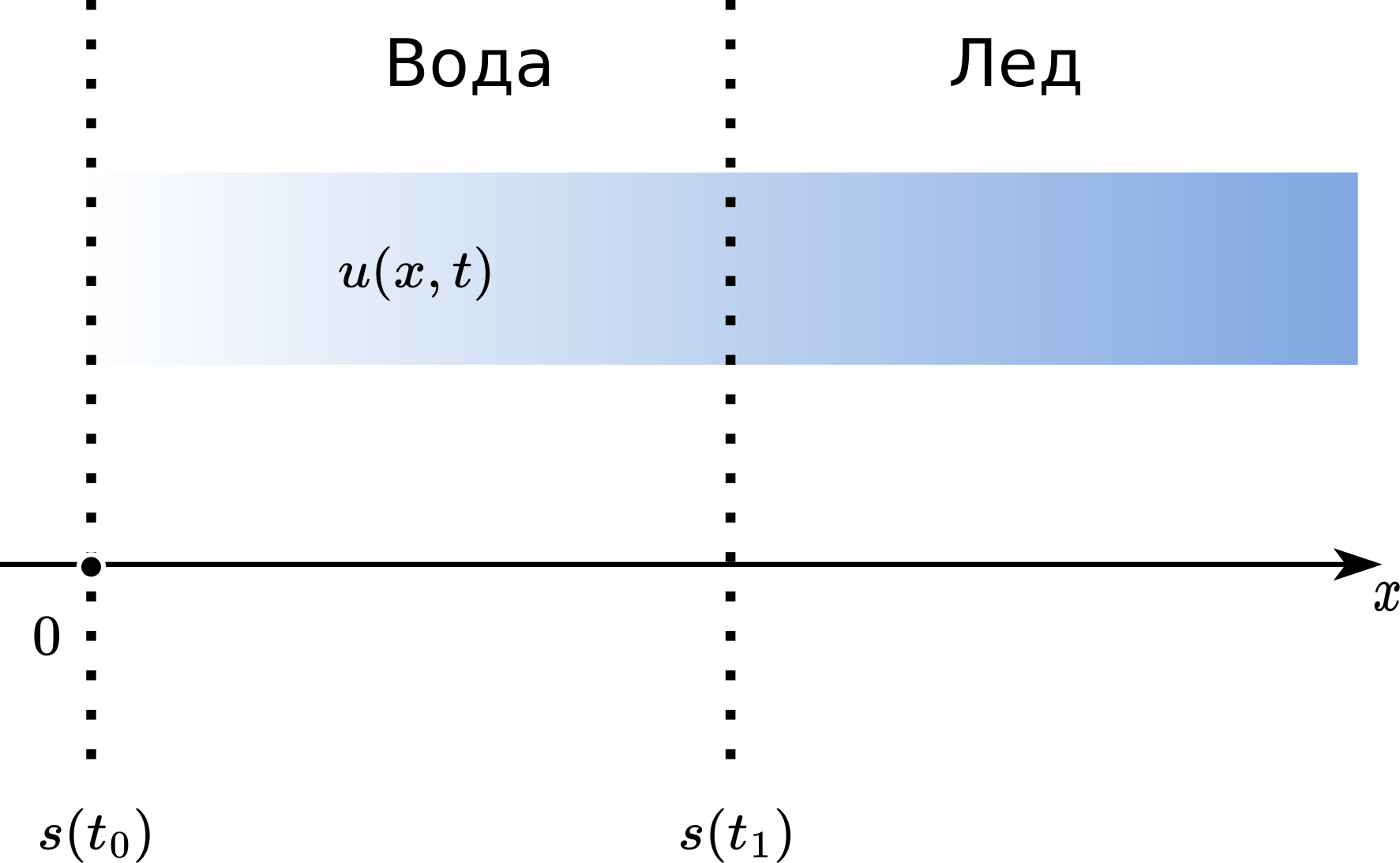
../_images/stefann.png

Сл. 10 Стефанов проблем у једној димензији. \(s(t)\) означава покретну границу, а \(u(x,t)\) температуру течне фазе (за \(x<s\)).

Дистрибуција температуре \(u(x,t)\) у региону у коме влада течно стање \(0 \le x \le s(t)\) дата је топлотном једначином:

\[\frac{\partial u}{\partial t} = \alpha \cdot \frac{\partial^2 u}{\partial x^2},\]

која може да се напише на следећи начин:

(14)\[\frac{\partial u}{\partial t} - \alpha \cdot \frac{\partial^2 u}{\partial x^2} = 0,\]

под следећим граничним условима:

(15)\[\begin{split}u(x,t) = e^{\alpha t}, \quad x = 0, \quad t > 0 \\ u(x,t) = 1,\quad x = s(t), \quad t > 0.\end{split}\]

Овде \(\alpha\), као и у претходним примерима означава физички параметар који комбинује топлотну проводност, густину и специфичну топлоту. Позиција покретне границе дата је једначином која је позната као Стефанов услов:

(16)\[\frac{1}{\alpha} \cdot \frac{ds}{dt} = - \frac{\partial u}{\partial x}, \quad x = s(t), \quad t > 0.\]

У општем случају, почетни услов за положај границе фаза дат је са:

(17)\[s(0) = 0.\]

За овако постављен проблем познато је и аналитичко решење, и то:

\[\begin{split}u(x,t) = e^{\alpha t - x} \\ s(t) = \alpha t.\end{split}\]

Решавање овог проблема НМПФЗ приступом подразумева конструкцију две неуронске мреже. Прва ће апроксимирати дистрибуцију температура \(u(x,t)\) док ће друга апроксимирати положај слободне границе између фаза \(s(t)\). Апроксимативна решења биће аутоматски диференцирана у односу на улазне варијабле од којих зависе, за вредности дефинисане скупом колокационих тачака из домена \(\lbrack 0,T\rbrack \times \mathcal{D}\), где је \(\mathcal{D \subset}\mathbb{R}^{d}\) ограничени домен, а \(T\) означава коначно време симулације. Функција губитка састоји се из компоненти изведених из (14), (15) и (17), користећи апроксимације за \(u\) и \(s\) у колокационим тачкама, које покривају како унутрашњост домена, тако и домене у којима важе почетни и гранични услови.

Конструкција функције губитка

Као што је већ речено, прва мрежа апроксимира функцију температуре \(u(x,t)\), а друга мрежа апроксимира положај слободне границе између фаза \(s(t)\). Функција губитка састоји се из разлике \(u\) и \(s\) и њихових апроксимација \(\widehat{u}\) и \(\widehat{s}\) које даје НМПФЗ и који представљају резидууме које даје главна диференцијална једначина, почетни и гранични услови. Дакле, укупан губитак \(\mathcal{L}\) одређен је сумом резидуума:

(18)\[\mathcal{L} = \mathcal{L}_r + \mathcal{L}_0 + \mathcal{L}_{b_{1}} + \mathcal{L}_{b_{2}} + \mathcal{L}_{b_{3}},\]

где су:

(19)\[\begin{split}\mathcal{L}_r = \frac{1}{N_r}\sum_{i = 1}^{N_r}{\left| \frac{\partial\widehat{u}(x,t)}{\partial t} - \alpha\frac{\partial^{2}\widehat{u}(x,t)}{\partial x^2} \right|^2}, \\ \mathcal{L}_0 = \frac{1}{N_{0}}\sum_{i = 1}^{N_0}{\left| \widehat{s}(0) - s(0) \right|^2}, \\ \mathcal{L}_{b_1} = \frac{1}{N_{b_1}}\sum_{i = 1}^{N_{b_1}}\left| \frac{1}{a}\frac{\partial\widehat{s}(t)}{\partial t} + \frac{\partial\widehat{u}}{\partial\widehat{s}(t)} \right|^2, \\ \mathcal{L}_{b_2} = \frac{1}{N_{b_2}}\sum_{i = 1}^{N_{b_2}}\left| \widehat{u}(0,t) - u(0,t) \right|^{2}, \\ \mathcal{L}_{b_3} = \frac{1}{N_{b_3}}\sum_{i = 1}^{N_{b_3}}\left| \widehat{u}\left( \widehat{s}(t),t \right) - u\left( s(t),t \right) \right|^2.\end{split}\]

Први члан \(\mathcal{L}_r\) пенализује по главној диференцијалној једначини (14), где је \(N_r\) величина batch-a колокационих тачака које се случајно узоркују из домена простор-временских координата које узимају вредности \(0 \leq x \leq 1\) и \(0s \leq t \leq 0,5s\), респективно. \(\widehat{u}(x,t)\) је апроксимативна неуронска мрежа температурског поља \(u(x,t)\). Други члан \(\mathcal{L}_0\) одређује испуњеност граничног услова (17). Испуњеност Стефановог граничног услова (16) дат је резидуумом \(\mathcal{L}_{b_1}\), где \(\widehat{s}(t)\) означава НМПФЗ апроксимацију положаја покретне границе. Последња два члана \(\mathcal{L}_{b_2}\) и \(\mathcal{L}_{b_3}\) одређују резидуале граничних услова (15), где \(N_0, \, N_{b_1}, \, N_{b_2}\), и \(N_{b_3}\) означавају број колокационих тачака у којима важе почетни и гранични услови.

Имплементација

Решење које користи функционалност већ познате библиотеке SCIANN дато је у следећем листингу:

Листинг 3 Решење Стефановог проблема у 1Д коришћењем SCIANN библиотеке
 1alpha = 1.0
 2
 3# Pocetni uslovi
 4t0 = 0.1
 5s0 = alpha * t0
 6
 7# Varijable
 8x = sn.Variable('x')
 9t = sn.Variable('t')
10u = sn.Functional (["u"], [x, t], 3*[30] , 'tanh')
11s = sn.Functional (["s"], [t], 3*[30] , 'tanh')
12
13# Glavna dif. jednacina
14L1 =  diff(u, t) - alpha * diff(u, x, order=2)
15
16TOLX=0.004
17TOLT=0.002
18
19# Stefanov uslov
20C1 = (1/alpha*diff(s, t) + diff(u,x)) * (1 + sign(x - (s-TOLX))) * (1-sign(x-s))
21# Pocetno s u trenutku t=t0
22C2 = ( s - s0 ) * (1-sign(t - (t0+TOLT)))
23# Granicni uslov za u kada je x=0
24C3 = ( u - exp(alpha*t) ) * (1-sign(x - (0 +TOLX)))
25# Temperatura na granici izmedju faza je 1
26C4 = (u-1) * (1-sign(x - (s+TOLX))) * (1+sign(x-s))
27
28x_data, t_data = [], []
29
30# Trening skup
31x_train, t_train = np.meshgrid(
32    np.linspace(0, 1, 300),
33    np.linspace(t0, 0.5, 300)
34)
35
36x_data, t_data = np.array(x_train), np.array(t_train)
37
38m = sn.SciModel([x, t], [L1,C1,C2,C3,C4], 'mse', 'Adam')
39h = m.train([x_data, t_data], 5*['zero'], learning_rate=0.002, batch_size=1024, epochs=200, adaptive_weights={'method':'NTK', 'freq':20})
40
41# Test
42x_test, t_test = np.meshgrid(
43    np.linspace(0, 1, 30),
44    np.linspace(0.01, 0.5, 30)
45)
46u_pred = u.eval(m, [x_test, t_test])
47s_pred = s.eval(m, [x_test, t_test])
48
49s=[]
50for e in s_pred:
51    s.append(e[0])

На почетку (линије 1-11) постављамо константе и варијабле. Приметимо да моделовање креће од временског тренутка \(t_0=0,1s\). Прва заграда у изразу за C1

C1 = (1/alpha*diff(s, t) + diff(u,x)) * (1 + sign(x - (s-TOLX))) * (1-sign(x-s))

представља сам Стефанов услов. Као што је уобичајено за постављање граничних услова, друга заграда поставља правило где тај гранични услов важи. За C1 је тај израз мало компликованији због толеранције, али заправо представља услов да је \(x \approx s\). Услов

C2 = ( s - s0 ) * (1-sign(t - (t0+TOLT)))

дефинише положај границе у почетном тренутку. Даље, услов

C3 = ( u - exp(alpha*t) ) * (1-sign(x - (0 +TOLX)))

поставља динамички услов промене температуре у тачки \(x=0\) према једначини (15). Коначно, последљи услов

C4 = (u-1) * (1-sign(x - (s+TOLX))) * (1+sign(x-s))

у истом скупу колокационих тачака као што је то био случај са условом C1, тј. на граници између фаза \(x \approx s\) поставља вредност температуре на 1. Остатак кода је мање-више стандардно тренирање, формирање тестног скупа и екстракција података о кретању границе s кроз време. Кретање границе између фаза кроз време може се видети на Сл. 11, док се поље температуре \(u(x,t=0,5)\) може видети на Сл. 12.

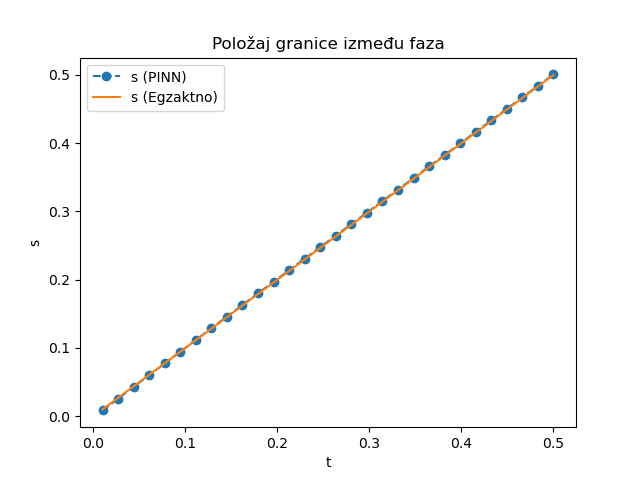
../_images/stefan-s.png

Сл. 11 Кретање границе између фаза \(s(t)\) током времена.

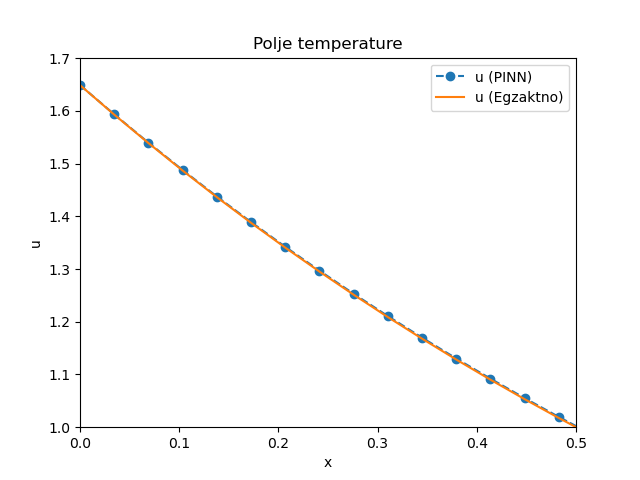
../_images/stefan-u.png

Сл. 12 Поље температура \(u(x,t)\) у тренутку \(t=0,5\)

Са дијаграма је очигледно да се НМПФЗ (PINN) решења у задовољавајућој мери слажу са аналитичким решењем за посматрану појаву. У складу са претходном општом дискусијом о употребној вредности НМПФЗ приступа, код директних проблема као што је овај, додатна вредност у односу на класичне нумеричке методе може се наћи у једноставнијој формулацији. Међутим, тек код инверзних проблема, када су и неки од параметара недовољно познати, приступ учења пропагацијом уназад показује своју праву снагу. Следећи одељак уводи непознати параметар у овај исти проблем.

Инверзни 1-Д Стефанов проблем

Претпоставим идентичну поставку Стефановог проблема, осим што сада није позната вредност материјалног параметра \(\alpha\), па тиме ни потпуни облик диференцијалне једначине, али је зато познато да је, на пример, у тренутку \(t=0,2\) граница између фаза уочена на координати \(x=0,2\). Непознати параметар увешћемо формулацијом:

# Nepoznati parametar
alpha = sn.Parameter(2.5, inputs=[x,t])

Параметру је дата почетна вредност од 2,5 и постављена зависност од обе улазне варијабле \(x\) и \(t\). Додатни гранични услов C5 дат је стандардно:

# Dodatni uslov u tacki s(t=0.2)=0.2
C5 = (1-sign(t - (0.2+TOLT))) * (1+sign(t-0.2)) * (s-0.2)

Иако је овог пута потребно нешто више епоха у процесу тренинга, јер је почетна вредност непознатог параметра \(\alpha\) (2,5) прилично далеко од реалне вредности (1), алгоритам који користи брзину учења од 0,001 у стотинак епоха долази до вредности \(\alpha=0,99\) и заиста задовољавајућег поклапања са аналитичким решењем, као што се види на Сл. 13 за кретање границе и за поље температуре у \(u(x,t=0,5)\) на Сл. 14.

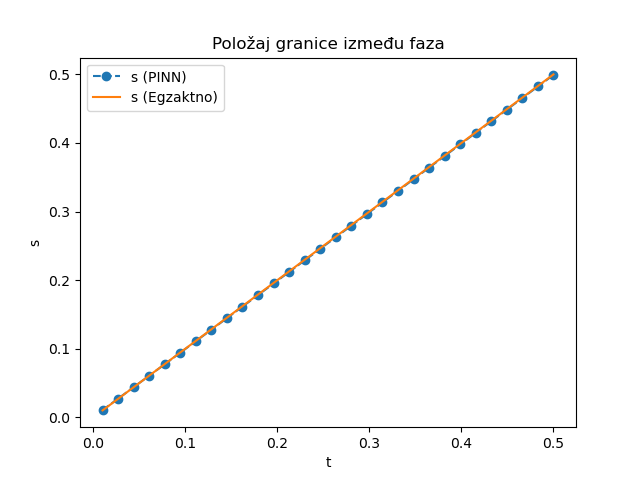
../_images/stefan-inv-s.png

Сл. 13 Кретање границе између фаза \(s(t)\) током времена за инверзни проблем

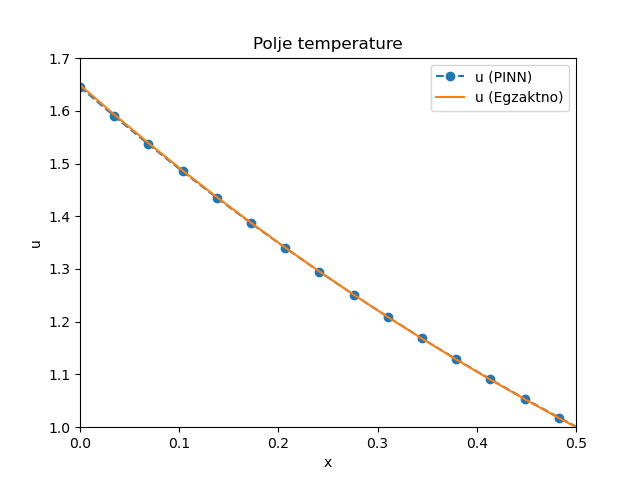
../_images/stefan-inv-u.png

Сл. 14 Поље температура \(u(x,t)\) у тренутку \(t=0,5\) за инверзни проблем