Rešavanje na domenu oblika kvadrata

Krenućemo od najjednostavnijeg dvodimenzionog slučaja stojećeg talasa u akustici. Za talasni broj \(k_0=2 \pi n\) za \(n=2\), treba rešiti Helmholcovu (Helmholtz) jednačinu oblika:

\[-\frac{\partial^2 u}{\partial x^2} - \frac{\partial^2 u}{\partial y^2} - k_0^2 u = f, \quad \Omega=[0,1]^2,\]

uz Dirihleove granične uslove

\[u(x,y)=0, \quad (x,y) \in \partial \Omega\]

prikazane na Sl. 37 i član koji specificira izvor \(f(x,y)=k_0^2 \sin(k_0x) \sin(k_0 y)\).

../_images/akustika1.png

Sl. 37 Postavka problema i granični uslovi.

Postoji analitičko rešenje ovog problema i ono glasi:

\[u(x,y) = \sin(k_0 x) \sin(k_0 y).\]

Za više detalja u pogledu teorijske pozadine diferencijalne jednačine i graničnih uslova čitalac može konsultovati Ihlenburg [Ihl98]. Rešenje metodom konačnih elemenata (MKE) je takođe dostupno u okviru Dolfinx tutorijala.

Implementacija

Rešenje direktnog problema prikazano je na sledećem listingu.

Listing 8 Rešenje problema prostiranja stojećeg talasa u 2D korišćenjem DeepXDE biblioteke
 1import deepxde as dde
 2import numpy as np
 3
 4# Frekvencija
 5n = 2
 6
 7precision_train = 10
 8precision_test = 30
 9weights = 100
10iterations = 10000
11learning_rate, num_dense_layers, num_dense_nodes, activation = 1e-3, 3, 150, "sin"
12
13# Uvezi sinus
14from deepxde.backend import tf
15sin = tf.sin
16
17# Osnovna PDE
18def pde(x, u):
19    du_xx = dde.grad.hessian(u, x, i=0, j=0)
20    du_yy = dde.grad.hessian(u, x, i=1, j=1)
21
22    f = k0 ** 2 * sin(k0 * x[:, 0:1]) * sin(k0 * x[:, 1:2])
23    return -du_xx - du_yy - k0 ** 2 * u - f
24
25# Egzaktno resenje
26def func(x):
27    return np.sin(k0 * x[:, 0:1]) * np.sin(k0 * x[:, 1:2])
28
29# Da li je kol. tacka na granici?
30def boundary(_, on_boundary):
31    return on_boundary
32
33# Geometrija jedinicnog kvadrata
34geom = dde.geometry.Rectangle([0, 0], [1, 1])
35# Talasni broj
36k0 = 2 * np.pi * n
37# Talasna duzina
38wave_len = 1 / n
39
40hx_train = wave_len / precision_train
41nx_train = int(1 / hx_train)
42
43hx_test = wave_len / precision_test
44nx_test = int(1 / hx_test)
45
46# Dirihleov granicni uslov y=0 na granicama
47bc = dde.icbc.DirichletBC(geom, lambda x: 0, boundary)
48
49data = dde.data.PDE(
50    geom,
51    pde,
52    bc,
53    num_domain=nx_train ** 2,
54    num_boundary=4 * nx_train,
55    solution=func,
56    num_test=nx_test ** 2,
57)
58
59# Mreza i model
60net = dde.nn.FNN([2] + [num_dense_nodes] * num_dense_layers + [1], activation, "Glorot uniform")
61model = dde.Model(data, net)
62
63# Forsiraj vece tezine za granicne uslove nego za unutrasnjost domena
64loss_weights = [1, weights]
65
66model.compile("adam", lr=learning_rate, metrics=["l2 relative error"], loss_weights=loss_weights)
67
68losshistory, train_state = model.train(iterations=iterations)
69dde.saveplot(losshistory, train_state, issave=True, isplot=True)

Nakon standardnog importa odgovarajućih modula, počinjemo specifikacijom opštih parametara. Ovaj primer ima par specifičnosti u odnosu na ostale. Naime, da bi se uspešno modelovale talasne pojave pomoću NMPFZ, gustina kolokacionih tačaka mora da bude direktno proporcionalna frekvenciji. Što je viša frekvencija n, manja je talasna dužina wave_len, pa je potrebno više kolokacionih tačaka da pokrije domen. Ovde smo uzeli 10 kolokacionih tačaka po talasnoj dužini tokom treninga i 30 tačaka po talasnoj dužini u test skupu.

# Frekvencija talasa
n = 2
precision_train = 10
precision_test = 30
weights = 100
learning_rate, num_dense_layers, num_dense_nodes, activation = 1e-3, 3, 150, "sin"

Takođe, vidimo da koristimo arhitekturu sa manjim brojem slojeva, ali sa više neurona po sloju, kao i aktivacionu funkciju \(\sin(x)\) koja bi trebalo da bude pogodnija za oponašanje talasnih fenomena.

Sledi specifikacija same parcijalne diferencijalne jednačine u obliku funkcije gubitka kako smo to već navikli:

def pde(x, u):
    du_xx = dde.grad.hessian(u, x, i=0, j=0)
    du_yy = dde.grad.hessian(u, x, i=1, j=1)

    f = k0 ** 2 * sin(k0 * x[:, 0:1]) * sin(k0 * x[:, 1:2])
    return -du_xx - du_yy - k0 ** 2 * u - f

Ovde koristimo uslužnu funkciju dde.grad.hessian odabirom koordinate koja se diferencira i kojom se diferencira. U ovom primeru su granični uslovi elementarni, pa ih ovde nećemo posebno navoditi.

Geometrija, talasni broj \(k_0=2 \pi \nu\) i talasna dužina \(\lambda=\frac{1}{\nu}\) daju se kao:

geom = dde.geometry.Rectangle([0, 0], [1, 1])
k0 = 2 * np.pi * n
wave_len = 1 / n

Jedina specifičnost koju dodatno treba naglasiti je da ponekad treba forsirati poštovanje graničnih uslova time što ćemo članu funkcije gubitka koji se odnosi na Dirihleov granični uslov dobiti veću težinu u odnosu na član koji se odnosi na diferencijalnu jednačinu.

weights = 100
loss_weights = [1, weights]
model.compile("adam", lr=learning_rate, metrics=["l2 relative error"], loss_weights=loss_weights)

Da bi se izbegao ovaj korak koji sa sobom nosi eksperimentisanje sa različitim vrednostima težinskog faktora, granični uslov se kod DeepXDE može zadavati i direktnom transformacijom funkcije gubitka, ali ovde se time nećemo baviti.

Rezultati

Nakon 10.000 epoha obučavanja optimizacionom metodom Adam koji je protekao kao što je prikazano na Sl. 38, dobijamo stojeći talas čiji 3D prikaz možemo videti na Sl. 39.

../_images/rezultati1-loss.png

Sl. 38 Tok obučavanja NMPFZ

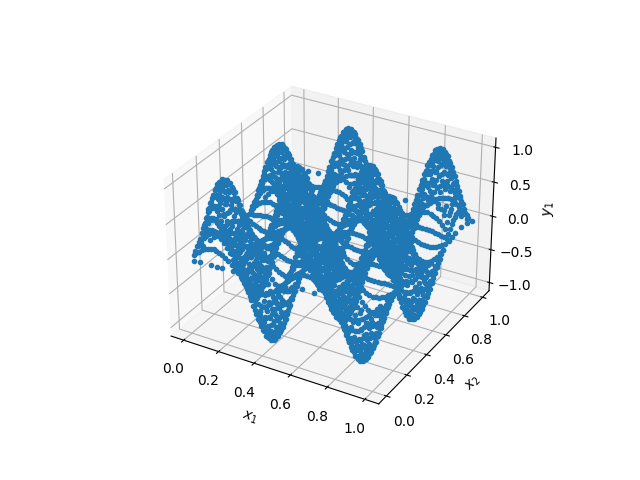
../_images/rezultati1.png

Sl. 39 Trodimenzioni prikaz talasa u domenu oblika kvadrata

Mera greške modela RMSE (Root Mean Squared Error) iznosi \(7,98 \cdot 10^{-2}\). Uz obraćanje posebne pažnje na forsiranje graničnih uslova, zatim arhitekturu NMPFZ i najzad tip aktivacione funkcije, uspeli smo da dobijemo prilično dobro rešenje. Čitalac može samostalno da proba kako bi promena frekvencije (a samim tim i talasne dužine), gustine kolokacionih tačaka, arhitekture, uticala na proces obučavanja modela.

Ovde možemo dati i kratku preporuku kako pristupiti modelovanju složenijih pojava, sa složenijom geometrijom i kompleksnijim graničnim uslovima. Pošto NMPFZ rešavanje zavisi od većeg broja hiper-parametara, preporuka je da se prvo reši do kraja pojednostavljen problem baziran na istoj diferencijalnoj jednačini, ali sa jednostavnijom geometrijom i graničnim uslovima. Kada se stekne slika o tome koja kombinacija hiper-parametara vodi do konvergencije rešenja, onda je lakše pristupiti glavnom, kompleksnom problemu. S druge strane, postoji nekoliko alata koji pretragu hiper-parametara čine efikasnijom, kao već pomenuti BlackFox koji koristi distribuirani genetski algoritam.