Rešavanje na domenu oblika kvadrata sa šupljinom

U odnosu na prethodni primer Rešavanje na domenu oblika kvadrata dodajemo šupljinu u sredini kvadratnog domena i propisujemo odgovarajuće Nojmanove granične uslove na obodu šupljine. Da se podsetimo, domen problema \(\Omega\) je kvadrat stranice \(L, \, L=1\), iz koga isključujemo krug poluprečnika \(R=\frac{1}{4}\). Za talasni broj \(k_0=2 \pi n\) i \(n=1\), rešavamo Helmholcovu jednačinu:

\[-\frac{\partial^2 u}{\partial x^2} - \frac{\partial^2 u}{\partial y^2} - k_0^2 u = f, \quad \text{ u } \Omega,\]

gde je član koji specificira izvor \(f(x,y)=k_0^2 \sin(k_0x) \sin(k_0 y)\). Oblik domena može se videti na Sl. 40.

Sl. 40 Postavka problema i granični uslovi

Postoji analitičko rešenje ovog problema i ono glasi:

\[u(x,y) = \sin(k_0 x) \sin(k_0 y).\]

Ovde ćemo specificirati Dirihleove granične uslove prema analitičkom rešenju na spoljnoj granici domena \(\Omega\) koju označavamo sa \(\Gamma_{outer}\):

\[u(x,y) \left| \right. \Gamma_{outer} = \sin(k_0 x) \sin(k_0 y), \quad (x,y) \in \Gamma_{outer}\]

Na sličan način, možemo da definišemo granični uslov na unutrašnjoj granici, ovog puta Nojmanov:

(30)\[(\nabla u \left| \right. \Gamma_{inner} \cdot n) (x,y) = \left[ k_0 \cos(k_0 x) \sin(k_0 y), k_0 \sin(k_0 x) \cos(k_0 y) \right] \cdot n = g(x,y),\]

gde je \(n\) vektor normale. Konciznije napisano, Nojmanov granični uslov na unutrašnjoj granici glasi:

\[\nabla u \left| \right. \Gamma_{inner} \cdot n = g.\]

Implementacija

Na sledećem listingu su dati glavni detalji implementacije. Namerno su izostavljeni delovi koji su irelevantni za samo rešavanje, kao što je crtanje dijagrama. Celokupna skripta se, kao i ostale, nalazi u repozitorijumu sa primerima.

Listing 9 Rešenje problema prostiranja stojećeg talasa u 2D domenu sa šupljinom

import deepxde as dde
import matplotlib.pyplot as plt
import numpy as np
from deepxde.backend import tf
sin = tf.sin

# Opsti parametri
n = 2
length = 1
R = 1 / 4

precision_train = 15
precision_test = 30

weight_inner = 10
weight_outer = 100
iterations = 5000
learning_rate = 1e-3
num_dense_layers = 3
num_dense_nodes = 350
activation = "sin"

k0 = 2 * np.pi * n
wave_len = 1 / n

# Parcijalna diferencijalna jednacina
def pde(x, y):
    dy_xx = dde.grad.hessian(y, x, i=0, j=0)
    dy_yy = dde.grad.hessian(y, x, i=1, j=1)
    f = k0**2 * sin(k0 * x[:, 0:1]) * sin(k0 * x[:, 1:2])
    return -dy_xx - dy_yy - k0**2 * y - f

# Egzaktno resenje
def func(x):
    return np.sin(k0 * x[:, 0:1]) * np.sin(k0 * x[:, 1:2])

# Da li je tacka na granici?
def boundary(_, on_boundary):
    return on_boundary

# Njumanovi granicni uslovi prema egzaktnom resenju
def neumann(x):
    grad = np.array([
            k0 * np.cos(k0 * x[:, 0:1]) * np.sin(k0 * x[:, 1:2]),
            k0 * np.sin(k0 * x[:, 0:1]) * np.cos(k0 * x[:, 1:2]),])

    normal = -inner.boundary_normal(x)
    normal = np.array([normal]).T
    result = np.sum(grad * normal, axis=0)
    return result

# Geometrija
outer = dde.geometry.Rectangle([-length / 2, -length / 2], [length / 2, length / 2])
inner = dde.geometry.Disk([0, 0], R)

# Da li je tacka na spoljnoj granici?
def boundary_outer(x, on_boundary):
    return on_boundary and outer.on_boundary(x)

# Da li je tacka na unutrasnjoj granici?
def boundary_inner(x, on_boundary):
    return on_boundary and inner.on_boundary(x)

# Iskljuci krug iz kvadrata
geom = outer - inner

hx_train = wave_len / precision_train
nx_train = int(1 / hx_train)

hx_test = wave_len / precision_test
nx_test = int(1 / hx_test)

# Na unutrasnjoj granici Njuman, na spoljnoj Dirihleovi
bc_inner = dde.icbc.NeumannBC(geom, neumann, boundary_inner)
bc_outer = dde.icbc.DirichletBC(geom, func, boundary_outer)

data = dde.data.PDE(
    geom,
    pde,
    [bc_inner, bc_outer],
    num_domain=nx_train**2,
    num_boundary=16 * nx_train,
    solution=func,
    num_test=nx_test**2,
)

net = dde.nn.FNN(
    [2] + [num_dense_nodes] * num_dense_layers + [1], activation, "Glorot uniform"
)

model = dde.Model(data, net)

loss_weights = [1, weight_inner, weight_outer]
model.compile("adam", lr=learning_rate, metrics=["l2 relative error"], loss_weights=loss_weights)

losshistory, train_state = model.train(iterations=iterations)

Koristićemo Tensorflow kao backend u svim našim primerima, ali treba imati u vidu da okvir DeepXDE podržava i PyTorch i još neke. Nakon standardne specifikacije opštih parametara i hiper-parametara, kao u primeru Rešavanje na domenu oblika kvadrata, uz jedinu modifikaciju dodavanja nešto više neurona po sloju (350), definišemo Nojmanov granični uslov prema jednačini (30):

def neumann(x):
    grad = np.array([
            k0 * np.cos(k0 * x[:, 0:1]) * np.sin(k0 * x[:, 1:2]),
            k0 * np.sin(k0 * x[:, 0:1]) * np.cos(k0 * x[:, 1:2]),])

    normal = -inner.boundary_normal(x)
    normal = np.array([normal]).T
    result = np.sum(grad * normal, axis=0)
    return result

Kao što se vidi iz koda, postoje uslužne funkcije koje računaju normale na pravilne granice u kolokacionim tačkama. Ponderske težine graničnih uslova u obuci weight_inner i weight_outer takođe spadaju u neku vrstu hiper-parametara, pa i njima treba posvetiti pažnju uz nekoliko manuelnih proba. Dalje, sledi specifikacija geometrije problema kao razlike kvadrata i diska:

outer = dde.geometry.Rectangle([-length / 2, -length / 2], [length / 2, length / 2])
inner = dde.geometry.Disk([0, 0], R)
geom = outer - inner

Ostatak skripte je sličan primeru bez šupljine Rešavanje na domenu oblika kvadrata, pa ga nećemo dodatno pojašnjavati. Dovoljno je reći da pažnju treba obratiti da bude dovoljno kolokacionih tačaka na spoljnoj i na unutrašnjoj granici.

Rezultati

Dobijeni rezultati su prikazani u formi konturnog grafika na Sl. 41. Oko unutrašnje granice prikazani su pravci vektora normala.

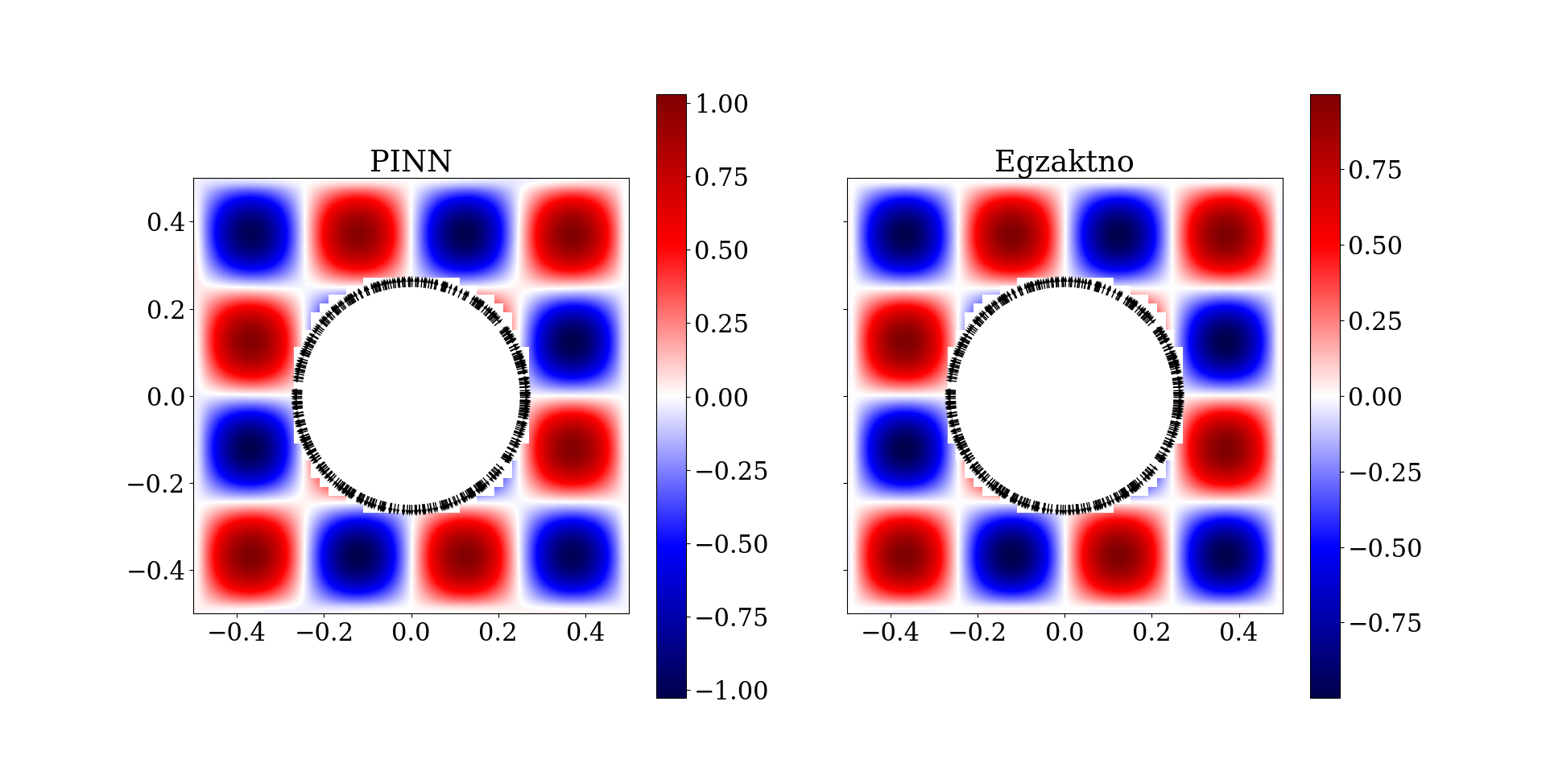
Sl. 41 Rezultati primera kvadratnog domena sa šupljinom

Mera relativne greške modela iznosi 0,048. Uz obraćanje posebne pažnje na forsiranje graničnih uslova, zatim arhitekturu NMPFZ i najzad tip aktivacione funkcije, uspeli smo da dobijemo prilično dobro rešenje. Čitalac može samostalno da proba kako bi promena frekvencije (a samim tim i talasne dužine), gustine kolokacionih tačaka, arhitekture, uticala na proces obuke modela.