Dvodimenzioni problem sa sočivom
Ovaj odeljak se bavi nešto modifikovanim primerom iz tutorijala za poznati softverski okvir za rad sa metodom konačnih elemenata Deal.II. Prvobitna svrha ovog primera je da simulira svojstva fokusiranja ultrazvučnog talasa koji generiše sočivo pretvarača sa promenljivom geometrijom. Savremene primene u medicinskom imidžingu koriste ultrazvučne talase ne samo za svrhe snimanja, već i za izazivanje određenih lokalnih efekata u materijalu, kao što su promene u optičkim svojstvima, koje se zatim mogu meriti drugim tehnikama snimanja. Vitalni sastojak ovih metoda je sposobnost fokusiranja intenziteta ultrazvučnog talasa u određenom delu materijala, idealno u tački, kako bi se mogla ispitati svojstva materijala na toj lokaciji.
Karakteristična talasna dužina ultrazvuka nešto manja od fenomena koje smo do sada modelovali metodom NMPFZ, te bi nam bio potreban izuzetno veliki broj kolokacionih tačaka što produžava treniranje. Zato smo talasnu dužinu nešto povećali (smanjili frekvenciju), dok ostale parametre nismo menjali.
Kako bismo izveli jednačine za ovaj problem, zvuk uzimamo kao talas kojim se širi promena pritiska:
gde je \(c\) brzina zvuka, koja se zbog jednostavnosti uzima kao konstanta, \(U = U(x,t) ,\; x \in \Omega, \; t \in \mathrm{R}\). Postavka problema data je na Sl. 42.

Sl. 42 Postavka problema i granični uslovi
Granica \(\Gamma=\partial\Omega\) podeljena je na dva dela, i to \(\Gamma_1\) i \(\Gamma_2 = \Gamma\setminus\Gamma_1\), gde \(\Gamma_1\) predstavlja sočivo, a \(\Gamma_2\) apsorbujuću granicu. Zapravo, želimo da napravimo takav granični uslov na \(\Gamma_2\) tako da se oponaša znatno veći domen. Na \(\Gamma_1\), pretvarač generiše talase konstantne frekvencije \(\omega > 0\) i konstantne jedinične amplitude:
Pošto nema drugih (internih ili graničnih) izvora i pošto samo izvor emituje talase frekvencije \(\omega\), dozvoljeno je da izvršimo razdvajanje promenljivih \(U(x,t) = \textrm{Re}\left(u(x)\,e^{i\omega t})\right)\). Kompleksna funkcija \(u(x)\) opisuje prostornu zavisnost amplitude i faze (relativno u odnosu na izvor) talasa frekvencije \(\omega\), dok je amplituda veličina koja nas interesuje. Ako ovako formulisanu funkciju uvrstimo u talasnu jednačinu, vidimo da za \(u\) imamo
Da bismo našli odgovarajuće granične uslove na \(\Gamma_2\) koji oponašaju apsorbujuću granicu, razmotrimo talas oblika \(V(x,t)=e^{i(k\cdot x - \omega t)}\) frekvencije \(\omega\) koji se prostire u pravcu \(k \in {\mathrm{R}^2}\). Da bi \(V\) bio rešenje talasne jednačine, mora da važi \(|k|=\frac{\omega}{c}\). Pretpostavimo da talas dolazi do \(x_0 \in \Gamma_2\) pod pravim uglom, na primer \(n=\frac{k}{|k|}\) gde \(n\) označava normalu na \(\Omega \in x_0\). Onda u \(x_0\), ovaj talas zadovoljava jednačinu
Postavljanjem graničnog uslova
talasi koji udaraju u granicu \(\Gamma_2\) pod pravim uglom biće savršeno apsorbovani. Sa druge strane, oni delovi talasnog polja koji ne padaju pod pravim uglom ne zadovoljavaju ovaj uslov, pa će dolaziti do parcijalnih refleksija. U osnovi, direktni delovi talasa će proći kroz granicu kao da ona ne postoji, dok će ostali biti reflektovani nazad u domen.
Ukoliko smo spremni da prihvatimo ovako predloženu aproksimaciju, onda za \(u\) važi sledeće:
prepoznajemo Helmholcovu jednačinu sa Dirihleovim uslovom na \(\Gamma_1\) i mešanim graničnim uslovom na \(\Gamma_2\). Zbog uslova na \(\Gamma_2\) ne možemo da tretiramo realne i imaginarne delove \(u\) posebno. Ono što možemo da uradimo je da formiramo sistem od dve parcijalne diferencijalne jednačine u kojima figurišu realni i imaginarni deo \(u\), sa graničnim uslovima na \(\Gamma_2\) koje vezuju ove dve komponente. Ako označimo da je \(v=\textrm{Re}\;u,\; w=\textrm{Im}\;u\), sistem (31) glasi:
Dakle, prve dve jednačine važe u celom domenu \(\Omega\), druge dve na granici \(\Gamma_2\), a poslednje dve na \(\Gamma_1\). Ovde prvi put imamo sistem diferencijalnih jednačina, ali ni to ne bi trebalo da bude problem za NMPFZ pristup, ako podrazumevamo da je sistem zatvoren, tj. jednoznačan.
Implementacija
Na osnovu sistema jednačina (32) treba da formiramo kompozitnu funkciju gubitka, da formiramo NMPFZ mrežu i da je istreniramo na dovoljnom broju kolokacionih tačaka. Evo ključnih delova implementacije ostvarene pomoću okvira SCIANN:
1import numpy as np
2import matplotlib.pyplot as plt
3import sciann as sn
4from numpy import pi
5from sciann.utils.math import diff, sign, sin, sqrt
6
7# Brzina talasa
8c = 1
9# Frekvencija
10omega = 2*pi*4
11
12x = sn.Variable('x')
13y = sn.Variable('y')
14v, w = sn.Functional (["v", "w"], [x, y], 3*[200] , 'sin')
15
16# Diferencijalne jednacine za v i w
17L1 = -omega**2 * v - c**2 * diff(v, x, order=2) - c**2 * diff(v, y, order=2)
18L2 = -omega**2 * w - c**2 * diff(w, x, order=2) - c**2 * diff(w, y, order=2)
19
20TOL = 0.015
21
22# Dirihleov uslov na G1 (y=0 i 0.4<x<0.6)
23a,b,c,d = 0.39762422, -1.57715550, -0.03696364, 1.60337246
24C1 = (1 - sign(y - (a + b*x + c*sqrt(x) + d*x**2 + TOL))) * (1 + sign(x-0.4)) * (1 - sign(x-0.6)) * (1-v)
25C2 = (1 - sign(y - (a + b*x + c*sqrt(x) + d*x**2 + TOL))) * (1 + sign(x-0.4)) * (1 - sign(x-0.6)) * (w-0)
26
27# Gornja granica G2 (gde je y=1)
28C3 = (1+sign(y - (1-TOL))) * ( c*diff(v,y) - omega*w )
29C4 = (1+sign(y - (1-TOL))) * ( c*diff(w,y) + omega*v )
30
31# Desna granica G2 (gde je x=1)
32C5 = (1+sign(x - (1-TOL))) * ( c*diff(v,x) - omega*w )
33C6 = (1+sign(x - (1-TOL))) * ( c*diff(w,x) + omega*v )
34
35# Leva granica G2 (gde je x=0)
36C7 = (1-sign(x - (0+TOL))) * ( -c*diff(v,x) - omega*w )
37C8 = (1-sign(x - (0+TOL))) * ( -c*diff(w,x) + omega*v )
38
39# Donja granica G2 (gde je y=0) i (x<0.4 or x>0.6)
40C9 = (1-sign(y - (0+TOL))) * ( (1 - sign(x-0.4)) + (1 + sign(x-0.6)) ) * ( -c*diff(v,y) - omega*w )
41C10 = (1-sign(y - (0+TOL))) * ( (1 - sign(x-0.4)) + (1 + sign(x-0.6)) ) * ( -c*diff(w,y) + omega*v )
42
43x_data, y_data = [], []
44
45kolokacione_tacke = np.genfromtxt('kolokacione_tacke.txt', delimiter=" ")
46
47for e in kolokacione_tacke:
48 ind, x1, y1 = e
49 x_data.append(x1)
50 y_data.append(y1)
51
52x_data, y_data = np.array(x_data), np.array(y_data)
53
54# Model i obucavanje
55m = sn.SciModel([x, y], [L1,L2,C1,C2,C3,C4,C5,C6,C7,C8,C9,C10], 'mse', 'Adam')
56h = m.train([x_data, y_data], 12*['zero'], learning_rate=0.001, batch_size=1024, epochs=8000, adaptive_weights={'method':'NTK', 'freq':200})
57
58# Test
59x_test, y_test = np.meshgrid(
60 np.linspace(0, 1, 200),
61 np.linspace(0, 1, 200)
62)
63v_pred = v.eval(m, [x_test, y_test])
64w_pred = w.eval(m, [x_test, y_test])
Nakon uobičajenih importa paketa, formiramo NMPFZ mreže za realni deo \(v\) i imaginarni deo \(w\) nepoznate funkcije \(u\). I ovde ćemo ići sa aktivacionom funkcijom \(\sin(x)\). Interesantan deo koda je definisanje graničnog uslova na \(\Gamma_1\) prema poslednje dve jednačine u sistemu (32):
a,b,c = 0.39762422, -1.57715550, 1.60337246
C1 = (1 - sign(y - (a + b*x + c*x**2 + TOL))) * (1 + sign(x-0.4)) * (1 - sign(x-0.6)) * (1-v)
C2 = (1 - sign(y - (a + b*x + c*x**2 + TOL))) * (1 + sign(x-0.4)) * (1 - sign(x-0.6)) * (w-0)
Jednačina \(y = a + b \cdot x + c \cdot x^2\) predstavlja jednačinu spoljne linije sočiva \(\Gamma_1\), u kojoj su koeficijenti \(a,b,c\) dobijeni fitovanjem. Dakle, prva zagrada u graničnim uslovima znači da uzimamo kolokacione tačke koje pripadaju tankom pojasu iznad linije \(\Gamma_1\), dok druga i treća zagrada imaju nenultu vrednost samo ako je \(0,4 < x < 0,6\).
Granični uslovi C3, C4, C5, C6, C7, C8 se odnose na mešanu formulaciju prema druge dve jednačine u sistemu (32) i važe na \(\Gamma_2\). Na primer:
C5 = (1+sign(x - (1-TOL))) * ( c*diff(v,x) - omega*w )
C6 = (1+sign(x - (1-TOL))) * ( c*diff(w,x) + omega*v )
se odnosi na desnu granicu gde je x=1 i uzima kolokacione tačke koje se nalaze u tankom pojasu širine TOL sa leve strane te granice.
Komponente funkcije gubitka C9 i C10 odnose se takođe na granicu \(\Gamma_2\), ali na liniji gde je \(y=0`\) i \(x < 0,4\) ili \(x > 0,6\):
C9 = (1-sign(y - (0+TOL))) * ( (1 - sign(x-0.4)) + (1 + sign(x-0.6)) ) * ( -c*diff(v,y) - omega*w )
C10 = (1-sign(y - (0+TOL))) * ( (1 - sign(x-0.4)) + (1 + sign(x-0.6)) ) * ( -c*diff(w,y) + omega*v )
Ovim smo kompletirali svih 12 komponenti funkcije gubitka. Pošto ih ima toliko, nije jednostavno izvršiti njihovo ponderisanje, odnosno dodelu težina svakoj komponenti. U ovakvim situacijama pomažu metode za adaptivno određivanje težina komponenti tokom obuke. U našem rešenju:
h = m.train([x_data, y_data], 12*['zero'], learning_rate=0.001, batch_size=1024, epochs=8000, adaptive_weights={'method':'NTK', 'freq':200})
upotrebili smo inovativnu metodu Neural Tangent Kernel (NTK) prema Wang et al. [WYP22]. Objašnjenje metode izlazi iz okvira ovog praktikuma, pa je nećemo detaljno razrađivati. Takođe, valja napomenuti da smo kolokacione tačke učitali iz posebnog fajla kolokacione_tacke.txt, koji je dobijen tako što smo ispisali čvorove konačnih elemenata koji se dobijaju iz generatora mreže paketa Deal.II.
Rezultati
Kao što je na početku odeljka već rečeno, primer je preuzet iz dokumentacije za paket koji se bavi analizom metodom konačnih elemenata Deal.II, tako da možemo da uporedimo rešenje za \(v=\textrm{Re}\;u\) koje smo dobili pomoću NMPFZ (Sl. 43) i rešenje koje se dobija klasičnom metodom konačnih elemenata (Sl. 44). Rešenje dobijeno MKE metodom možemo smatrati referentnim, jer je korišćena veoma gusta mreža i pokazana je konvergencija.
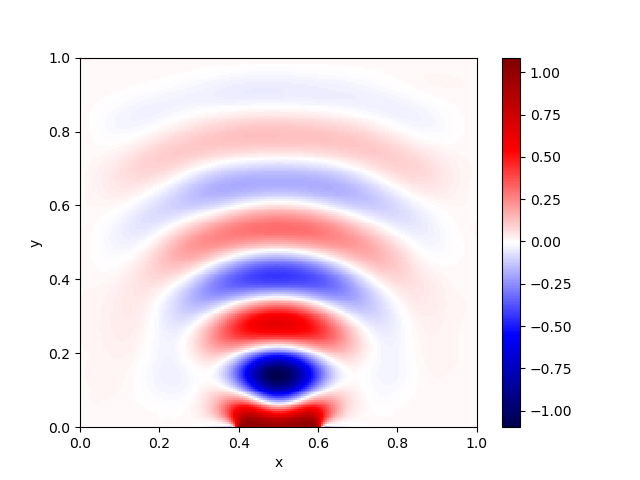
Sl. 43 Rešenje za \(v=\textrm{Re}\;u\) dobijeno pomoću NMPFZ
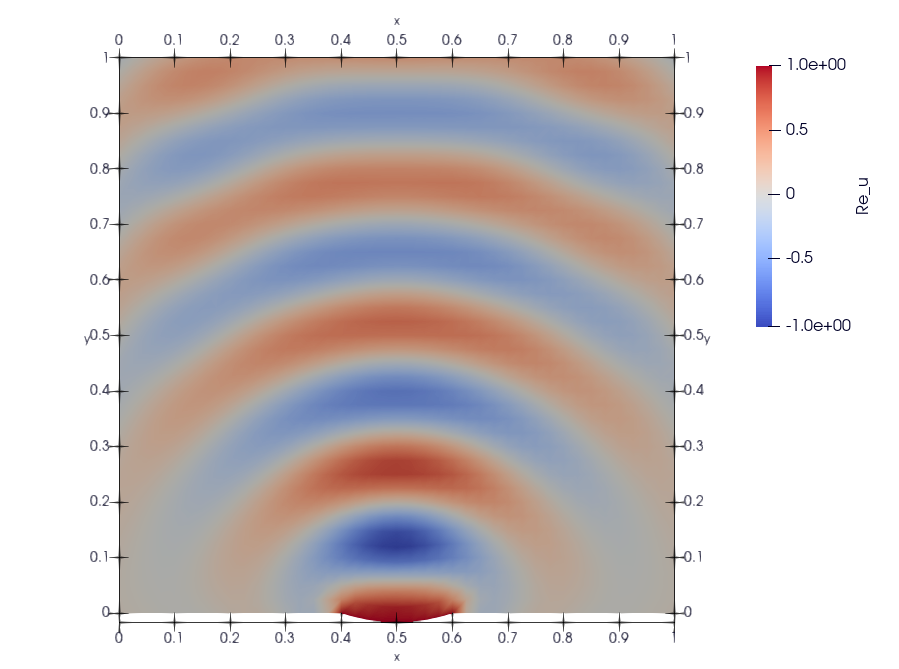
Sl. 44 Rešenje za \(v=\textrm{Re} \; u\) dobijeno metodom konačnih elemenata
Kvalitativno gledano, NMPFZ rešenje ima iste karakteristike kao MKE rešenje. Međutim, oko sočiva i prima granicama \(\Gamma_2\) očigledan je pad kvaliteta rešenja. Uzrok možemo tražiti na nekoliko mesta:
Prvo, kod MKE je izvor na liniji sočiva \(\Gamma_1\) moguće preciznije specificirati po samoj liniji, a ne u pojedinačnim tačkama kao kod NMPFZ.
Moguće je da 50.000 kolokacionih tačaka nije dovoljno za obučavanje.
Primećeno je da obučavanje optimizacionim algoritam
Adamne može da spusti vrednost gubitka ispod neke granice. Ovde verovatno treba eksperimentisati sa varijabilnom stopom učenja, ili dodati neki drugi optimizator kao u primeru Propagacija talasa u otvorenom kanalu.
Dalje eksperimentisanje na ovom primeru ostavljamo čitaocu.