Primer proračuna proizvodnje
Analitički model
U ovom odeljku ćemo upotrebiti metodologiju prikazanu u Uvod i jednostavni model PVWatts objašnjen u Osnovne jednačine modela upotrebiti na jednom realnom primeru. U pitanju je solarna elektrana u Centralnoj Srbiji sa 146 instalisanih panela na krovu jedne zgrade. Sve karakteristike instalacije su nam poznate (ugao nagiba, azimut, vrsta panela, karakteristike invertora i slično). Od podataka imamo i serije temperature vazduha i komponenti osunčanosti, tako da lako možemo analitički, po jednačinama (35), (36) i (37) da izračunamo proizvodnju. U slučaju da posedujemo vremensku prognozu, možemo približno i da predvidimo buduću proizvodnju koristeći standardni PVWatts model.
Iako matematika nije komplikovana, za programsku implementaciju ovog analitičkog modela koristićemo pomoć biblioteke PVLIB Holmgren et al. [HHM18]. Na narednom listingu prikazan je deo koda koji se tiče učitavanja, pripreme podataka i izvođenja PVWatts modela.
1import numpy as np
2import pandas as pd
3import pvlib
4from pvlib.location import Location
5
6# Ucitaj podatke o vremenu i proizvodnji
7solcast_data = pd.read_csv("data_21.08.16_22.10.14.csv", index_col="Time")
8solcast_data.index = pd.to_datetime(solcast_data.index, dayfirst=True)
9
10# Nagib, azimut i lokacija panela
11surface_tilt = 7
12surface_azimuth = 290
13location = Location(latitude=43.905410, longitude=20.341986, altitude=243, tz="Europe/Belgrade", name="Pons Cacak")
14
15# Pomeri vreme za pola sata, izracunaj poziciju sunca u svakom trenutku
16times = solcast_data.index - pd.Timedelta('30min')
17solar_position = location.get_solarposition(times)
18solar_position.index += pd.Timedelta('30min')
19
20# Novi dataframe sa vrednostima za vrednosti osuncanosti DNI, GHI, DHI
21df_poa = pvlib.irradiance.get_total_irradiance(
22 surface_tilt=surface_tilt,
23 surface_azimuth=surface_azimuth,
24 dni=solcast_data['DNI'],
25 ghi=solcast_data['GHI'],
26 dhi=solcast_data['DHI'],
27 solar_zenith=solar_position['apparent_zenith'],
28 solar_azimuth=solar_position['azimuth'],
29 model='isotropic')
30
31# Izvuci ukupnu POA vrednost iz df_poa
32E_data = df_poa["poa_global"]
33# Izvuci temperaturu vazduha
34T_data = solcast_data["Tamb"]
35# Izvuci proizvodnju P
36P_data = solcast_data["P"]
37
38# Nedelju dana za treniranje
39E_data_train = E_data.loc["2021-10-31":"2021-11-06"]
40T_data_train = T_data.loc["2021-10-31":"2021-11-06"]
41P_data_train = P_data.loc["2021-10-31":"2021-11-06"]
42
43# Sledecih nedelju dana za testiranje
44E_data_test = E_data.loc["2021-11-07":"2021-11-13"]
45T_data_test = T_data.loc["2021-11-07":"2021-11-13"]
46P_data_test = P_data.loc["2021-11-07":"2021-11-13"]
47
48#
49# Parametri modela
50#
51pdc0 = 0.375 # nominal power [kWh]
52Tref = 25.0 # cell reference temperature
53gamma_pdc = -0.005 # influence of the cell temperature on PV system
54pdc0_inv = 50
55eta_inv_nom = 0.96
56eta_inv_ref = 0.9637
57pac0_inv = eta_inv_nom * pdc0_inv # maximum inverter capacity
58a = -2.98 # cell temperature parameter
59b = -0.0471 # Wind coefficient
60E0 = 1000 # reference irradiance
61deltaT = 1 # cell temperature parameter
62num_of_panels = 146 # Broj panela u instalaciji
63
64#
65# Originalni PVWAtts model
66#
67def orig_pvwatts_model(x):
68 Ta = x[:,0:1] # Temperatura vazduha
69 E = x[:,1:2] # Ukupna POA osuncanost
70
71 Tm = E * np.exp(a+b*2) + Ta # Brzina vetra uzeta kao prosecna od 2 m/s
72 Tc = Tm + E/E0*deltaT
73 P_dc_temp = ((Tc-Tref) * gamma_pdc + 1.)
74 P_dc = (E * 1.e-03 * pdc0 * P_dc_temp) * num_of_panels
75 zeta = (P_dc+1.e-2)/pdc0_inv
76
77 eta = eta_inv_nom/eta_inv_ref * (-0.0162*zeta - 0.0059/zeta + 0.9858)
78 eta[eta<0] = 0.
79 ac = np.minimum(eta*P_dc, pac0_inv)
80
81 return ac
Nakon standardnih importa biblioteka, učitavamo satne serije podataka o vremenu:
Ta- temperatura vazduha,DNI,GHI,DHI- komponente osunčanosti
i podatke o proizvodnji P u Pandas okvir. Na žalost, nemamo dostupne podatke o brzini vetra na lokaciji, pa ćemo tu komponentu uzeti kao prosečnu na tom podneblju, tj. vrednost od \(2\,m/s\). Funkcija pvlib.irradiance.get_total_irradiance() biblioteke PVLIB nam izračunava položaj sunca za bilo koji vremenski trenutak i bilo koju lokaciju na Zemlji, a na osnovu njega i ukupnu osunčanost panela čiji je položaj dat uglovima surface_tilt i surface_azimuth. Kao ulaz, ova metoda uzima komponente DNI, GHI i DHI definisane u odeljku Komponente zračenja.
Nakon ekstrakcije perioda od nedelju dana od 31. oktobra do 6. novembra i drugog perioda od 7. do 13. novembra, postavljamo sve parametre koji se koriste u jednačinama (35), (36) i (37), onako kako najbolje odgovara samoj instalaciji. Svi parametri osim tri su konstante prihvaćene u literaturi. Ta tri parametra čija vrednost može da se podešava su a i b iz izraza (35) i gamma_pdc iz izraza (36). Njihove vrednosti (-2,98, -0.0471 i -0,005 respektivno) zadajemo prema vrsti panela i načinu postavljanja instalacije.
Poređenje rezultata dobijenih čistim modelom i merenih vrednosti može se videti na Sl. 61. Očigledno je da postoji značajno odstupanje, tj. model daje više vrednosti od merenja. Koren srednje kvadratne greške (RMSE) iznosi čak 2,46 kW. Određeni doprinos ovako visokoj vrednosti greške sigurno je posledica činjenice da hlađenje panela usled uticaja vetra nismo uzeli u obzir usled nedostatka podataka o vetru.
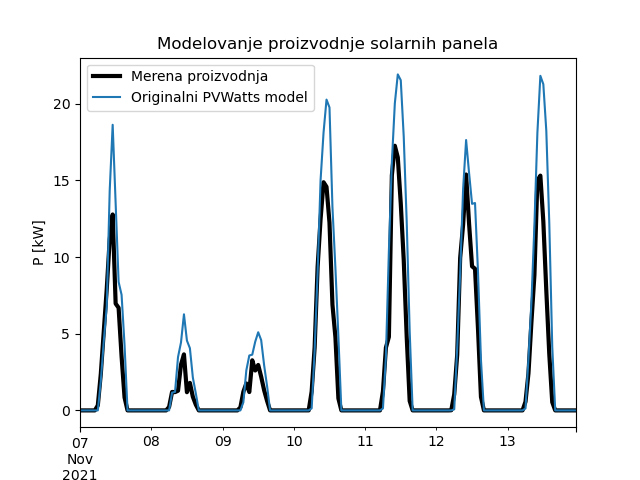
Sl. 61 Poređenje čistog PVWAtts modela sa merenom proizvodnjom
Nijedan model nije savršena slika stvarnosti i ne može da obuhvati sve faktore koji utiču na proizvodnju. Čak iako je model savršen (a ne može biti), moguće su pojave grešaka pri merenju temperature, osunčanosti, brzine vetra. Dalje, kod samog modela imamo više parametara čije vrednosti uzimamo iz literature i deklaracije proizvođača. Realne vrednosti tih parametara sigurno odstupaju od tih vrednosti i menjaju se tokom životnog veka uređaja.
Podešavanje parametra pomoću NMPFZ
Postavlja se pitanje da li vrednosti koje daje model mogu biti približnije realnim vrednostima samo podešavanjem parametara modela. Probaćemo da iskoristimo činjenicu da podatke o proizvodnji za nedelju od 31. oktobra imamo i da pomoću NMPFZ probamo da „pomirimo” izlaz analitičkog modela i merenja proizvodnje tako što ćemo parametar a jednačine (36) proglasiti nepoznatim. Osnovna ideja je da se NMPFZ trenira i jednačinom i podacima i da kao izlaz isporuči i model sa manjom greškom i novu, bolju vrednost parametra a.
Na sledećem listingu mogu se videti interesantni delovi implementacije ove ideje:
1# Parametar "a" pustamo da se trenira
2a_var = dde.Variable(-4.0)
3
4#
5# Jednacina koju koristi PINN
6#
7def pvwatts_eq(x, y):
8 Ta = x[:,0:1] # Temperatura vazduha
9 E = x[:,1:2] # Ukupna POA osuncanost
10
11 Tm = E * tf.exp(a_var+b*2) + Ta # Brzina vetra uzeta kao prosecna od 2 m/s
12 Tc = Tm + E/E0*deltaT
13 P_dc_temp = ((Tc-Tref) * gamma_pdc + 1)
14 P_dc = (E * 1.e-03 * pdc0 * P_dc_temp) * num_of_panels
15 zeta = (P_dc+1.e-2)/pdc0_inv
16
17 eta = eta_inv_nom/eta_inv_ref * (-0.0162*zeta - 0.0059/zeta + 0.9858)
18 eta = tf.maximum(0., tf.sign(eta)) * eta
19 ac = tf.minimum(eta*P_dc, pac0_inv)
20
21 return y - ac
22
23# Imamo 168 tacaka sa merenjima proizvodnje. Pripremi strukturu za PointSet granicni uslov
24train_points = np.zeros((168,2))
25train_measured_production = np.zeros((168,1))
26train_points[:,0] = T_data_train.to_numpy().T
27train_points[:,1] = E_data_train.to_numpy().T
28train_measured_production[:,0] = P_data_train.to_numpy().T
29
30# Imamo 168 tacaka sa merenjima za narednu nedelju za test
31test_points = np.zeros((168,2))
32test_measured_production = np.zeros((168,1))
33test_points[:,0] = T_data_test.to_numpy().T
34test_points[:,1] = E_data_test.to_numpy().T
35test_measured_production[:,0] = P_data_test.to_numpy().T
36
37# Minimumi i maksimumi T i E za kreiranje geometrije problema
38minT, maxT = min(train_points[:,0]), max(train_points[:,0])
39minE, maxE = min(train_points[:,1]), max(train_points[:,1])
40
41geom = dde.geometry.Rectangle([minT, minE], [maxT, maxE])
42bc_y = dde.icbc.PointSetBC(train_points, train_measured_production, component=0)
43
44# Isti broj kolokacionih tacaka za jednacinu i za granicne uslove. Moze i drugacije.
45data = dde.data.PDE(geom, pvwatts_eq, [bc_y], 168, 168, solution = orig_pvwatts_model, num_test=100)
46
47layer_size = [2] + [30] * 5 + [1]
48activation = "tanh"
49initializer = "Glorot uniform"
50net = dde.nn.FNN(layer_size, activation, initializer)
51
52variable_a = dde.callbacks.VariableValue(a_var, period=1000)
53model = dde.Model(data, net)
54
55model.compile(optimizer="adam", lr=0.001, metrics=["l2 relative error"], external_trainable_variables=[a_var])
56losshistory, train_state = model.train(iterations=20000, callbacks=[variable_a])
57predicted_test = model.predict(test_points)
58
59# Predikcije manje od nule nemaju smisla. Nuluj ih.
60predicted_test[predicted_test<0]=0
Kao i kod ranije obrađenih inverznih problema koji koriste biblioteku DeepXDE, postavljamo parametar kao varijablu čija se vrednost dobija procesom obučavanja:
a_var = dde.Variable(-4.0)
Ako pogledamo funkciju pvwatts_eq(x, y), ona je gotovo identična funkciji orig_pvwatts_model(x) sa Listing 12. Razlika je u tome što pvwatts_eq(x, y) ne vraća vrednost snage, već funkciju gubitka, kao što smo već navikli. Još jedna razlika ogleda se u korišćenju TensorFlow logike umesto uslovnog izraza:
eta = tf.maximum(0., tf.sign(eta)) * eta
Ovaj izraz nije ništa drugo nego uslov da ako imamo nefizičku vrednost eta<0 postavimo da je eta=0. Ovom formulacijom izbegavamo instrukciju uslovnog skoka, koja se na grafičkom procesoru izvodi dosta sporije od čistog računa u pokretnom zarezu.
U daljem toku programa treba da postavimo strukturu za poseban granični uslov PointSet, koji smo već koristili u odeljku Inverzni problem i Propagacija talasa u otvorenom kanalu:
train_points = np.zeros((168,2))
train_measured_production = np.zeros((168,1))
train_points[:,0] = T_data_train.to_numpy().T
train_points[:,1] = E_data_train.to_numpy().T
train_measured_production[:,0] = P_data_train.to_numpy().T
bc_y = dde.icbc.PointSetBC(train_points, train_measured_production, component=0)
Imamo ukupno 168 tačaka (7x24) merenja proizvodnje koje ćemo iskoristiti u pokušaju da „spustimo” vrednosti koje daje originalni model. Geometriju problema koji rešavamo definišemo opsegom ulaznih varijabli temperature i ukupne osunčanosti, koje se uzimaju iz tabele podataka. Onda možemo da postavimo i kolokacione tačke na domenu naredbom:
data = dde.data.PDE(geom, pvwatts_eq, [bc_y], 168, 168, solution = orig_pvwatts_model, num_test=100)
Za broj slučajnih kolokacionih tačaka unutar domena uzeli smo isti broj tačaka koliko imamo u PointSet graničnom uslovu. Nije nužno da broj tačaka bude jednak, pa ostavljamo čitaocu da eksperimentiše različitim vrednostima. Ostatak koda je manje-više isti kao kod svih drugih primera koji koriste DeepXDE za rešavanje inverznih problema. Tu je postavljanje arhitekture NMPFZ i hiper-parametara, algoritma optimizacije, stope obuke, callback funkcije za štampu trenutne vrednosti a_var tokom obuke i slično. Na kraju se anuliraju negativne vrednosti predviđene proizvodnje jer nemaju fizičkog smisla.